题目内容
 已知f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π).f′(x)如图,则f(x)表达式为
已知f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π).f′(x)如图,则f(x)表达式为
- A.2sin(
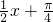 )
) - B.4sin(
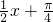 )
) - C.2sin(x
 )
) - D.4sin(x
 )
)
B
分析:由题意设导函数f′(x)=A′cos(ω′x+φ′),由图象求得f′(x)的解析式,经验证可得答案.
解答:由题意设导函数f′(x)=A′cos(ω′x+φ′),由图象可得A′=2,
由 =
= 可得ω′=
可得ω′= ,故f′(x)=2cos(
,故f′(x)=2cos( x+φ′),
x+φ′),
代入点( ,0)可解得φ′=
,0)可解得φ′= ,故f′(x)=2cos(
,故f′(x)=2cos( x+
x+ ),
),
对四个选项进行验证可知:只有选项B求导数后等于2cos( x+
x+ ),
),
故选B
点评:本题考查由图象求三角函数的图象,涉及导数问题,属基础题.
分析:由题意设导函数f′(x)=A′cos(ω′x+φ′),由图象求得f′(x)的解析式,经验证可得答案.
解答:由题意设导函数f′(x)=A′cos(ω′x+φ′),由图象可得A′=2,
由
 =
= 可得ω′=
可得ω′= ,故f′(x)=2cos(
,故f′(x)=2cos( x+φ′),
x+φ′),代入点(
 ,0)可解得φ′=
,0)可解得φ′= ,故f′(x)=2cos(
,故f′(x)=2cos( x+
x+ ),
),对四个选项进行验证可知:只有选项B求导数后等于2cos(
 x+
x+ ),
),故选B
点评:本题考查由图象求三角函数的图象,涉及导数问题,属基础题.

练习册系列答案
相关题目
 已知f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π).f′(x)如图,则f(x)表达式为( )
已知f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π).f′(x)如图,则f(x)表达式为( )