题目内容
已知:f(x)=acosx+bcos2x+1
(1)若g(x)=f(x)-acosx+2(b>0),将函数y=g(x)的图象左移
个单位得函数y=h(x)的图象,求函数y=h(x)的周期与单调增区间;
(2)若b≤0,对任意x均有f(x)≥0恒成立,求a+b的最大值.
(1)若g(x)=f(x)-acosx+2(b>0),将函数y=g(x)的图象左移
| π | 12 |
(2)若b≤0,对任意x均有f(x)≥0恒成立,求a+b的最大值.
分析:(1)先求出 g(x)的解析式,根据函数y=Asin(ωx+∅)的图象变换规律求得函数h(x)的解析式,从而求出函数y=h(x)的周期与单调增区间.
(2)令t=cosx∈[-1,1],g(t)=2bt2+at+1-b(t∈[-1,1]),则g(t)≥0,再分当b=0、和当b<0两种情况,分别求出a+b的最大值,从而得出结论.
(2)令t=cosx∈[-1,1],g(t)=2bt2+at+1-b(t∈[-1,1]),则g(t)≥0,再分当b=0、和当b<0两种情况,分别求出a+b的最大值,从而得出结论.
解答:解:(1)∵g(x)=f(x)-acosx+2(b>0)=b•cos2x+3,将函数y=g(x)的图象左移
个单位得函数y=bcos2(x+
)+3=bcos(2x+
)+3的图象,
故h(x)=bcos(2x+
)+3(b>0).…1′
故函数y=h(x)的周期为π,由2kπ-π ≤2x+
≤ 2kπ,k∈z,可得kπ-
π≤x≤kπ-
,故单调增区间为(kπ-
π,kπ-
),(k∈Z).…6′
(2)因为b≤0,对任意x恒有f(x)≥0成立,则2bcos2x+acosx+1-b≥0
令t=cosx∈[-1,1],g(t)=2bt2+at+1-b(t∈[-1,1]),则有g(t)≥0.…7′
当b=0时,g(t)=at+1有g(1)≥0且g(-1)≥0,即-1≤a≤1,(a+b)max=1;…9′
当b<0时,g(t)=2bt2+at+1-b(t∈[-1,1])有:
,
即
,即-1≤a+b≤2b+1<1,…11′
综上可得:(a+b)max=1.…12′
| π |
| 12 |
| π |
| 12 |
| π |
| 6 |
故h(x)=bcos(2x+
| π |
| 6 |
故函数y=h(x)的周期为π,由2kπ-π ≤2x+
| π |
| 6 |
| 7 |
| 12 |
| π |
| 12 |
| 7 |
| 12 |
| π |
| 12 |
(2)因为b≤0,对任意x恒有f(x)≥0成立,则2bcos2x+acosx+1-b≥0
令t=cosx∈[-1,1],g(t)=2bt2+at+1-b(t∈[-1,1]),则有g(t)≥0.…7′
当b=0时,g(t)=at+1有g(1)≥0且g(-1)≥0,即-1≤a≤1,(a+b)max=1;…9′
当b<0时,g(t)=2bt2+at+1-b(t∈[-1,1])有:
|
即
|
综上可得:(a+b)max=1.…12′
点评:本题主要考查余弦函数的增区间,函数y=Asin(ωx+∅)的图象变换规律,求三角函数的最值,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知y=f(x)是偶函数,而y=f(x+1)是奇函数,且对任意0≤x≤1,都有f′(x)≥0,则a=f(
),b=f(
),c=f(
)的大小关系是( )
| 98 |
| 19 |
| 101 |
| 17 |
| 136 |
| 15 |
| A、c<a<b |
| B、c<b<a |
| C、a<c<b |
| D、a<b<c |
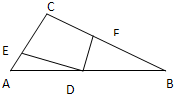 (1)如图,D是Rt△ABC的斜边AB上的中点,E和F分别在边AC和BC上,且ED⊥FD,求证:EF2=AE2+BF2(EF2表示线段EF长度的平方)(尝试用向量法证明)
(1)如图,D是Rt△ABC的斜边AB上的中点,E和F分别在边AC和BC上,且ED⊥FD,求证:EF2=AE2+BF2(EF2表示线段EF长度的平方)(尝试用向量法证明)