题目内容
8.定义在R上的函数y=f(x)满足f(x+2)=2f(x),且x∈(-1,1]时,$f(x)=-|x|+\frac{1}{2}$,则当x∈(0,7]时,y=f(x)与g(x)=log4x的图象的交点个数为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 根据函数的关系,求出函数在(0,7]上的解析式,作出函数f(x)与g(x)的图象,利用数形结合进行求解即可.
解答 解:∵f(x+2)=2f(x),且x∈(-1,1]时,$f(x)=-|x|+\frac{1}{2}$,
∴f(x)=2f(x-2),
若x∈(1,3],则x-2∈(-1,1],则f(x)=2f(x-2)=2(-|x-2|+$\frac{1}{2}$)=-2|x-2|+1,
若x∈(3,5],则x-2∈(1,3],则f(x)=2f(x-2)=2(-2|x-2-2|+1)=-4|x-4|+2,
若x∈(5,7],则x-2∈[3,5],则f(x)=2f(x-2)=2(-4|x-2-4|+2)=-8|x-6|+4,
作出函数f(x)和g(x)在∈(0,7]上的图象如图:
由图象知两个函数共有7个交点,
故选:B.
点评 本题主要考查函数与方程的应用,求出函数的解析式,利用数形结合是解决本题的关键.考查学生的作图能力.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
6.设a,b,c为三条不同的直线,α,β是两个不同的平面,则下列判断正确的是( )
| A. | 若a⊥b,b⊥c,则a⊥c | B. | 若a∥α,b∥α,则a∥b | C. | 若a∥α,b⊥α,则b∥α | D. | 若a⊥α,α∥β,则a⊥β |
3.已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{3}$=1(a>0)过点(-2,0),则双曲线的离心率为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
13.直线$\left\{\begin{array}{l}x=5-3t\\ y=3+\sqrt{3}t\end{array}\right.$(为参数)的倾斜角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
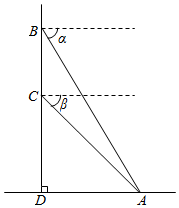 如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60m,则山高为30($\sqrt{3}$+1).
如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60m,则山高为30($\sqrt{3}$+1).