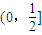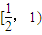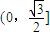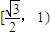题目内容

△ABC的顶点A的坐标为(1,4),∠B、∠C的角平分线的方程分别为x-2y=0和x+y-1=0,求BC所在直线的方程.

思路分析:由于三角形的顶点A坐标为(1,4),∠B、∠C的角平分线的方程分别为x-2y=0和x+y-1=0,所以点A关于直线x-2y=0和x+y-1=0的对称点A′和A″都在BC所在直线上,这条直线的方程通过运用直线方程的两点式不难求解.

解:设A关于直线x-2y=0的对称点为点A′(x1,y1),

则根据几何性质,它们应该满足的关系有:两点的中点在直线x-2y=0上.

两条直线连线垂直于直线x-2y=0.

列出式子即为:=0和·=-1,

解这两个式子,得x1=,y1=.

设A关于直线x+y-1=0的对称点为点A″(x2,y2),

同理可求得x2=-3,y2=0.

由几何性质,点A′和点A″应该都在BC所在直线上.应用直线方程的两点式容易求得这条直线的方程为4x+17y+1

练习册系列答案
相关题目
精英家教网如图，直角三角形ABC的顶点A的坐标为（-2，0），直角顶点B的坐标为（0，-2
2
），顶点C在x轴上．
（1）求BC边所在直线的方程．
（2）圆M是△ABC的外接圆，求圆M的方程．
椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的内接等腰△ABC的顶点A的坐标为（0，b），其底边BC上的高在y轴上，若△ABC的面积不超过
3
2
b2，则椭圆离心率的取值范围为（　　）
A、(0，
1
2
]
B、[
1
2
，1)
C、(0，
3
2
]
D、[
3
2
，1)
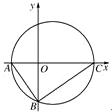已知△ABC的顶点A的坐标为（2，3），重心G的坐标为（2，-1），则BC边上的中点坐标是（　　）
如图，直角三角形ABC的顶点A的坐标为（-1，0），直角顶点B的坐标为(0，-
3
)，顶点C在x轴上．求：
（1）求点C的坐标及△ABC的外接圆M的方程；
（2）设△ABC的外接圆M的圆心为点M，另有一个定点N（-3，-4），作出一个以MN为直径，G为圆心的圆，记为圆G，圆M和圆G交于点P和点Q，直线NP，NQ是圆M的切线吗？请说明理由；
（3）求直线PQ的方程．
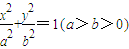椭圆的内接等腰△ABC的顶点A的坐标为（0，b），其底边BC上的高在y轴上，若△ABC的面积不超过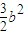，则椭圆离心率的取值范围为（ ）
A．
B．
C．
D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网