题目内容
椭圆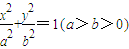 的内接等腰△ABC的顶点A的坐标为(0,b),其底边BC上的高在y轴上,若△ABC的面积不超过
的内接等腰△ABC的顶点A的坐标为(0,b),其底边BC上的高在y轴上,若△ABC的面积不超过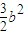 ,则椭圆离心率的取值范围为( )
,则椭圆离心率的取值范围为( )A.
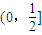
B.
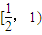
C.
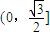
D.
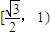
【答案】分析:首先设点B(acosx,bsintx) C(-acosx,bsinx),进而求得底边、高、面积得出恒有(1-sinx)cosx≤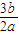 ,再根据c2=a2-b2,就能得到答案.
,再根据c2=a2-b2,就能得到答案.
解答:解:∵△ABC为等腰三角形.
∴可设点B(acosx,bsintx) C(-acosx,bsinx).其中-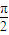 <x<
<x<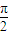 .
.
此时易知,该三角形底边BC=2acosx,高=b(1-sinx)
∴S=ab(1-sinx)cosx
由题设可得ab(1-sinx)cosx≤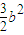
∴恒有(1-sinx)cosx≤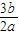
∴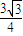 ≤
≤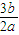
整理可得,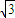 a≤2b
a≤2b
两边平方,3a2≤4b2=4(a2-c2)
∴4c2≤a2
∴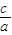 ≤
≤ .
.
故选A.
点评:本题考查了椭圆的简单性质,本题采用参数方法使问题变得简单化,属于中档题.
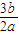 ,再根据c2=a2-b2,就能得到答案.
,再根据c2=a2-b2,就能得到答案.解答:解:∵△ABC为等腰三角形.
∴可设点B(acosx,bsintx) C(-acosx,bsinx).其中-
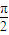 <x<
<x<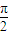 .
.此时易知,该三角形底边BC=2acosx,高=b(1-sinx)
∴S=ab(1-sinx)cosx
由题设可得ab(1-sinx)cosx≤
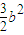
∴恒有(1-sinx)cosx≤
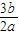
∴
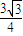 ≤
≤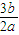
整理可得,
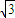 a≤2b
a≤2b两边平方,3a2≤4b2=4(a2-c2)
∴4c2≤a2
∴
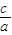 ≤
≤ .
.故选A.
点评:本题考查了椭圆的简单性质,本题采用参数方法使问题变得简单化,属于中档题.

练习册系列答案
相关题目
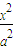 +
+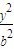 =1,(a>b>0)的长轴为AB,以AB为底边作椭圆的内接等腰梯形ABCD,求此等腰梯形面积的最大值.
=1,(a>b>0)的长轴为AB,以AB为底边作椭圆的内接等腰梯形ABCD,求此等腰梯形面积的最大值.