题目内容
已知钝角△ABC中,角A,B,C的对边分别为a,b,c,且(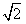 a-c)cosB=bcosC,
a-c)cosB=bcosC,
(Ⅰ)求角B的大小;
(Ⅱ)设向量m=(cos2A+1,cosA),n=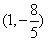 ,且m⊥n,求
,且m⊥n,求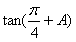 的值。
的值。
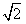 a-c)cosB=bcosC,
a-c)cosB=bcosC,(Ⅰ)求角B的大小;
(Ⅱ)设向量m=(cos2A+1,cosA),n=
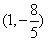 ,且m⊥n,求
,且m⊥n,求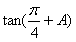 的值。
的值。 解:(Ⅰ)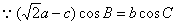 ,
,
由正弦定理,得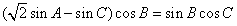 ,
,
∴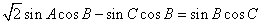 ,
,
即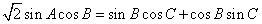 ,
,
∴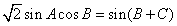 ,
,
∵在△ABC中,sin(B+C)=sinA,
∴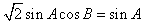 ,得
,得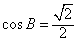 ,
,
∴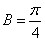 ;
;
(Ⅱ)∵m⊥n,则m·n=0,
即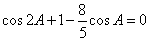 ,
,
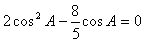 ,
,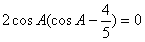 ,
,
∵cosA≠0,
∴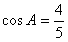 ,
,
由sin2A+cos2A=1,sinA>0,
∴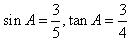 ,
,
则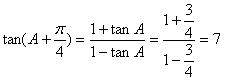 。
。
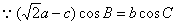 ,
,由正弦定理,得
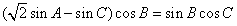 ,
, ∴
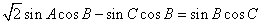 ,
,即
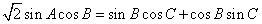 ,
,∴
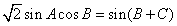 ,
, ∵在△ABC中,sin(B+C)=sinA,
∴
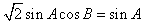 ,得
,得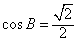 ,
,∴
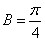 ;
;(Ⅱ)∵m⊥n,则m·n=0,
即
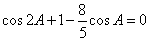 ,
,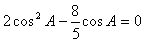 ,
,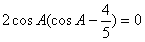 ,
, ∵cosA≠0,
∴
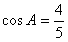 ,
,由sin2A+cos2A=1,sinA>0,
∴
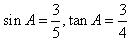 ,
,则
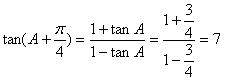 。
。 
练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目

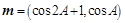 ,
, 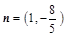 ,且m⊥n,求
,且m⊥n,求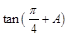 的值.
的值.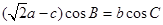
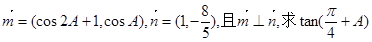 的值。
的值。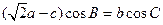

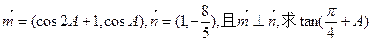 的值。
的值。