题目内容
已知钝角△ABC中,角A、B、C的对边分别为a、b、c,且有(| 2 |
(1)求角B的大小;
(2)设向量
| m |
| n |
| 8 |
| 5 |
| m |
| n |
| π |
| 4 |
分析:(1)利用正弦定理把题设等式中的边转换成角的正弦,然后利用两角和公式化简整理求得cosB的值,进而求得B.
(2)利用向量垂直的性质利用向量的坐标求得cos2A+1-
cosA=0,利用二倍角公式整理成关于cosA的一元二次方程求得cosA的值,利用同角三角函数的基本关系求得tanA的值,然后利用正切的两角和公式求得tan(A+
)的值.
(2)利用向量垂直的性质利用向量的坐标求得cos2A+1-
| 8 |
| 5 |
| π |
| 4 |
解答:解:(1)∵(
a-c)cosB=bcosC,
由正弦定理得:(
sinA-sinC)cosB=sinBcosC
∴
sinAcosB-sinCcosB=sinBcosC即
sinAcosB=sinBcosC+sinCcosB
∴
sinAcosB=sin(B+C)
因为在△ABC中sin(B+C)=sinA则
sinAcosB=sinA
∴cosB=
,B=
(2)∵
⊥
∴
•
=0即cos2A+1-
cosA=0
∴2cos2A-
cosA=0即2cosA(cosA-
)=0
∵cosA≠0∴cosA=
由sin2A+cos2A=1,sinA>0
∴sinA=
,tanA=
则tan(A+
)=
=
=7
| 2 |
由正弦定理得:(
| 2 |
∴
| 2 |
| 2 |
∴
| 2 |
因为在△ABC中sin(B+C)=sinA则
| 2 |
∴cosB=
| ||
| 2 |
| π |
| 4 |
(2)∵
| m |
| n |
| m |
| n |
| 8 |
| 5 |
∴2cos2A-
| 8 |
| 5 |
| 4 |
| 5 |
∵cosA≠0∴cosA=
| 4 |
| 5 |
由sin2A+cos2A=1,sinA>0
∴sinA=
| 3 |
| 5 |
| 3 |
| 4 |
| π |
| 4 |
| 1+tanA |
| 1-tanA |
1+
| ||
1-
|
点评:本题主要考查了正弦定理的应用,二倍角两角和公式的化简求值,同角三角函数的基本关系的应用.综合考查了学生对三角函数基础知识的掌握.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目

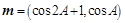 ,
, 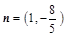 ,且m⊥n,求
,且m⊥n,求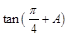 的值.
的值.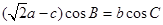
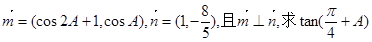 的值。
的值。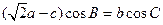

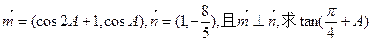 的值。
的值。