题目内容
已知钝角△ABC中，AB=2，AC=1，△ABC的面积为
，则
•
的值为（ ）
| ||
| 2 |
| AB |
| AC |
分析：由三角形的面积公式，列式算出sinA=
，得到A=
或
．当A=
时，利用余弦定理算出BC=
，从而证出
C=
，与已知条件△ABC为钝角三角形矛盾．由此可得A=
，利用数量积的公式加以计算，可得
•
的值．
| ||
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| 3 |
C=
| π |
| 2 |
| 2π |
| 3 |
| AB |
| AC |
解答：解：∵△ABC中，AB=2，AC=1，△ABC的面积为
，
∴S=
AB×ACsinA=
，即
×2×1×sinA=
，
解之得sinA=
，结合A∈（0，π）可得A=
或
∵当A=
时，BC=
=
，
∴此时cosC=
=
=0，得C=
，
这与△ABC为钝角三角形矛盾，可得A=
不符合题意．
因此A=
，可得
•
=
•
cosA=2×1×cos
=-1．
故选：D
| ||
| 2 |
∴S=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
解之得sinA=
| ||
| 2 |
| π |
| 3 |
| 2π |
| 3 |
∵当A=
| π |
| 3 |
| AB2+AC2-2AB•ACcosA |
| 3 |
∴此时cosC=
| AC2+BC2-BC2 |
| 2AC•BC |
| 3+1-4 | ||
2×
|
| π |
| 2 |
这与△ABC为钝角三角形矛盾，可得A=
| π |
| 3 |
因此A=
| 2π |
| 3 |
| AB |
| AC |
| |AB| |
| |AC| |
| 2π |
| 3 |
故选：D
点评：本题给出钝角三角形的两边和面积，求数量积
•
的值．着重考查了数量积计算公式、余弦定理、三角形的形状判断和三角形面积公式等知识，属于中档题．
| AB |
| AC |
练习册系列答案
相关题目
， 
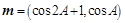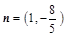，且m⊥n，求
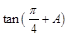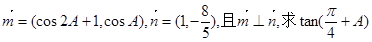的值．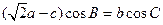
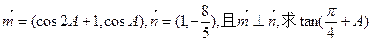的值。
的值。