题目内容
14.已知F1、F2为双曲线E的左、右焦点,点M在E上,△F1F2M为等腰三角形,且顶角为120°,则E的离心率为( )| A. | $\frac{\sqrt{5}+1}{2}$ | B. | $\frac{\sqrt{3}}{2}$+1 | C. | $\frac{\sqrt{3}+1}{2}$ | D. | $\frac{\sqrt{2}+1}{2}$ |
分析 不妨设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),由题意,∠F1F2M=120°,F1F2=F2M=2c,可得M(2c,$\sqrt{3}$c),代入$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,可得$\frac{4{c}^{2}}{{a}^{2}}$-$\frac{3{c}^{2}}{{b}^{2}}$=1,即可求出E的离心率.
解答 解:不妨设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),
由题意,∠F1F2M=120°,F1F2=F2M=2c,
∴M(2c,$\sqrt{3}$c),
代入$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,可得$\frac{4{c}^{2}}{{a}^{2}}$-$\frac{3{c}^{2}}{{b}^{2}}$=1,
∴4e4-8e2+1=0,
∴e=$\frac{\sqrt{3}+1}{2}$,
故选:C.
点评 本题考查双曲线的方程与性质,考查学生的计算能力,求出M的坐标是关键.

练习册系列答案
相关题目
2.下列条件使M与A,B,C一定共面的是( )
| A. | $\overrightarrow{OM}$=2$\overrightarrow{OA}$-$\overrightarrow{OB}$+$\overrightarrow{OC}$ | B. | $\overrightarrow{OM}$+$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$ | ||
| C. | $\overrightarrow{OM}$=$\frac{1}{5}$$\overrightarrow{OA}$+$\frac{2}{3}$$\overrightarrow{OB}$+$\frac{1}{2}$$\overrightarrow{OC}$ | D. | $\overrightarrow{MA}$+$\overrightarrow{MB}$+$\overrightarrow{MC}$=$\overrightarrow{0}$ |
9.函数f(x)=x2+x-lnx的零点的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
6.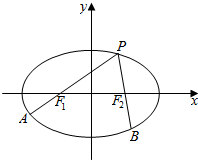 如图,F1F2为椭圆C:$\frac{{x}^{2}}{4}$$+\frac{{y}^{2}}{3}$=1的左、右焦点,点P为椭圆C上一点,延长PF1、,PF2分别交椭圆C于A,B.若$\overrightarrow{P{F}_{1}}$=2$\overrightarrow{{F}_{1}A}$,$\overrightarrow{P{F}_{2}}$=$λ\overrightarrow{{F}_{2}B}$,则λ=( )
如图,F1F2为椭圆C:$\frac{{x}^{2}}{4}$$+\frac{{y}^{2}}{3}$=1的左、右焦点,点P为椭圆C上一点,延长PF1、,PF2分别交椭圆C于A,B.若$\overrightarrow{P{F}_{1}}$=2$\overrightarrow{{F}_{1}A}$,$\overrightarrow{P{F}_{2}}$=$λ\overrightarrow{{F}_{2}B}$,则λ=( )
 如图,F1F2为椭圆C:$\frac{{x}^{2}}{4}$$+\frac{{y}^{2}}{3}$=1的左、右焦点,点P为椭圆C上一点,延长PF1、,PF2分别交椭圆C于A,B.若$\overrightarrow{P{F}_{1}}$=2$\overrightarrow{{F}_{1}A}$,$\overrightarrow{P{F}_{2}}$=$λ\overrightarrow{{F}_{2}B}$,则λ=( )
如图,F1F2为椭圆C:$\frac{{x}^{2}}{4}$$+\frac{{y}^{2}}{3}$=1的左、右焦点,点P为椭圆C上一点,延长PF1、,PF2分别交椭圆C于A,B.若$\overrightarrow{P{F}_{1}}$=2$\overrightarrow{{F}_{1}A}$,$\overrightarrow{P{F}_{2}}$=$λ\overrightarrow{{F}_{2}B}$,则λ=( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{4}$ |
3.如图,直线l经过第二、第三、第四象限,l的倾斜角为α,斜率为k,则( )


| A. | ksin(π+α)>0 | B. | kcos(π-α)>0 | C. | ksinα≤0 | D. | kcosα≤0 |