题目内容
在四棱锥P-ABCD中,BC∥AD,PA⊥PD,AD=2BC,AB=PB, E为PA的中点.
(1)求证:BE∥平面PCD;
(2)求证:平面PAB⊥平面PCD.
 |
证明:(1)取PD的中点F,连接EF,CF.
 因为E为PA的中点,所以EF∥AD,EF=
因为E为PA的中点,所以EF∥AD,EF=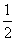 AD.
AD.
因为BC∥AD,BC=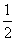 AD,
AD,
所以EF∥BC,EF=BC.
所以四边形BCFE为平行四边形.
所以BE∥CF.
因为BE平面PCD,CF平面PCD,
所以BE∥平面PCD.
(2)因为AB=PB,E为PA的中点,所以PA⊥BE.
因为BE∥CF,所以PA⊥CF.
因为PA⊥PD,PD平面PCD,CF平面PCD,PD∩CF=F,
所以PA⊥平面PCD.
因为PA平面PAB,所以平面PAB平面PCD.

练习册系列答案
相关题目
 ,②y=
,②y= (x+1),③y=|x-1|
(x+1),③y=|x-1| ,④y=2x+1,其中在区间(0,1)上单
,④y=2x+1,其中在区间(0,1)上单 ,D是BC边上任意一点(D与B、C不重合),且
,D是BC边上任意一点(D与B、C不重合),且 ,则
,则 等于 .
等于 .
 )∣(>0)的图象向左平移
)∣(>0)的图象向左平移 个单位后,所得图象对应的函数为偶函数 ,则实数的最小值是 .
个单位后,所得图象对应的函数为偶函数 ,则实数的最小值是 .
 (
( ,i为虚数单位),则
,i为虚数单位),则 的值为 .
的值为 . 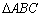 的三个顶点
的三个顶点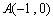 ,
,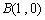 ,
,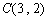 ,其外接圆为
,其外接圆为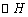 .
.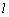 过点
过点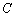 ,且被
,且被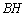 上的任意一点
上的任意一点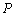 ,若在以
,若在以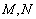 ,使得点
,使得点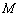 是线段
是线段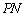 的中点,求
的中点,求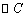 的半径
的半径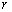 的取值范围.
的取值范围.
 ,其导函数为
,其导函数为
 .
.
 在
在
 处的切线
处的切线
 的方程;
的方程;