题目内容
已知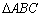 的三个顶点
的三个顶点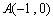 ,
,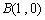 ,
,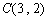 ,其外接圆为
,其外接圆为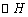 .
.
(1)若直线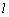 过点
过点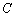 ,且被
,且被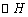 截得的弦长为2,求直线
截得的弦长为2,求直线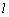 的方程;
的方程;
(2)对于线段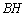 上的任意一点
上的任意一点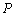 ,若在以
,若在以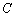 为圆心的圆上都存在不同的两点
为圆心的圆上都存在不同的两点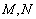 ,使得点
,使得点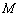 是线段
是线段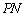 的中点,求
的中点,求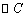 的半径
的半径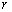 的取值范围.
的取值范围.
.(1)线段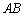 的垂直平分线方程为
的垂直平分线方程为 ,线段
,线段 的垂直平分线方程为
的垂直平分线方程为 ,
,
所以 外接圆圆心
外接圆圆心 ,半径
,半径 ,
,
圆 的方程为
的方程为 . ………………………………………………4分
. ………………………………………………4分
设圆心 到直线
到直线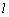 的距离为
的距离为 ,因为直线
,因为直线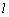 被圆
被圆 截得的弦长为2,所以
截得的弦长为2,所以 .
.
当直线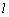 垂直于
垂直于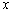 轴时,显然符合题意,即
轴时,显然符合题意,即 为所求;…………………………………6分
为所求;…………………………………6分
当直线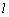 不垂直于
不垂直于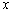 轴时,设直线方程为
轴时,设直线方程为 ,则
,则 ,解得
,解得 ,
,
综上,直线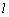 的方程为
的方程为 或
或 . ………………………………8分
. ………………………………8分
(2)直线 的方程为
的方程为 ,设
,设 ,
,
因为点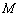 是线段
是线段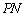 的中点,所以
的中点,所以 ,又
,又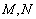 都在半径为
都在半径为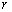 的圆
的圆 上,
上,
所以 即
即 …………………10分
…………………10分
因为该关于 的方程组有解,即以
的方程组有解,即以 为圆心,
为圆心,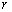 为半径的圆与以
为半径的圆与以 为圆心,
为圆心,
 为半径的圆有公共点,所以
为半径的圆有公共点,所以 ,…………12分
,…………12分
又 ,所以
,所以 对
对 ]成立.
]成立.
而 在上的值域为[
在上的值域为[ ,10],所以
,10],所以 且
且 .……15分
.……15分
又线段 与圆
与圆 无公共点,所以
无公共点,所以 对
对 成立,即
成立,即 .
.
故圆 的半径
的半径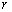 的取值范围为
的取值范围为 . …………………………16分
. …………………………16分

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
抽样统计甲,乙两个城市连续5天的空气质量指数(AQI),数据如下:
| 城市 | 空气质量指数(AQI) | ||||
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | |
| 甲 | 109 | 111 | 132 | 118 | 110 |
| 乙 | 110 | 111 | 115 | 132 | 112 |
则空气质量指数(AQI)较为稳定(方差较小)的城市为 (填甲或乙).
 ,则集合
,则集合 = .
= .
 ,
, ,则
,则 .
. B.
B. C.
C. D.
D.

 ,点
,点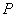 在
在 轴上,当
轴上,当  取最小值时,
取最小值时, B.
B. C.
C. D.
D.
 设
设
 是函数
是函数
 的导数,
的导数,
 的图像如图所示,则
的图像如图所示,则
 的图像最有可能的是( ).
的图像最有可能的是( ). 