题目内容
2.已知tan(α+$\frac{π}{4}$)=2,则$\frac{sin2α}{sin2a+co{s}^{2}α}$=$\frac{2}{5}$.分析 把已知的等式左边利用两角和与差的正切函数公式及特殊角的三角函数值化简,得到关于tanα的方程,求出方程的解得出tanα的值,利用同角三角函数关系对$\frac{sin2α}{sin2a+co{s}^{2}α}$进行变形并代入求值即可.
解答 解:由tan(α+$\frac{π}{4}$)=2得到:
tan(α+$\frac{π}{4}$)=$\frac{tanα+tan\frac{π}{4}}{1-tanαtan\frac{π}{4}}$=$\frac{1+tanα}{1-tanα}$=2,
解得tanα=$\frac{1}{3}$.
所以$\frac{sin2α}{sin2a+co{s}^{2}α}$=$\frac{2sinαcosα}{2sinαcosα+co{s}^{2}α}$=$\frac{2tanα}{2tanα+1}$=$\frac{2×\frac{1}{3}}{2×\frac{1}{3}+1}$=$\frac{2}{5}$.
故答案是:$\frac{2}{5}$.
点评 此题考查了同角三角函数间的基本关系,两角和与差的正切函数公式,熟练掌握公式是解本题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
12.设a=2-3,b=log35,c=cos100°,则( )
| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | c>b>a |
17.已知P(-1,2),过P点且与原点距离最大的直线的方程是( )
| A. | x+2y-5=0 | B. | 2x-y+5=0 | C. | x-2y+5=0 | D. | 2x+y-5=0 |
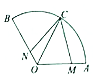 如图,扇形AOB所在圆的半径是1,弧AB的中点为C,动点M,N分别在OA,OB上运动,且满足OM=BN,∠AOB=120°.
如图,扇形AOB所在圆的半径是1,弧AB的中点为C,动点M,N分别在OA,OB上运动,且满足OM=BN,∠AOB=120°.