题目内容
【题目】小明准备利用暑假时间去旅游,妈妈为小明提供四个景点,九寨沟、泰山、长白山、武夷山.小明决定用所学的数学知识制定一个方案来决定去哪个景点:(如图)曲线![]() 和直线
和直线![]() 交于点
交于点![]() .以
.以![]() 为起点,再从曲线
为起点,再从曲线![]() 上任取两个点分别为终点得到两个向量,记这两个向量的数量积为
上任取两个点分别为终点得到两个向量,记这两个向量的数量积为![]() .若
.若![]() 去九寨沟;若
去九寨沟;若![]() 去泰山;若
去泰山;若![]() 去长白山;
去长白山; ![]() 去武夷山.
去武夷山.
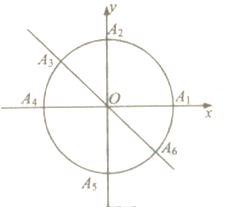
(1)若从![]() 这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;
这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;
(2)按上述方案,小明在曲线![]() 上取点
上取点![]() 作为向量的终点,则小明决定去武夷山.点
作为向量的终点,则小明决定去武夷山.点![]() 在曲线
在曲线![]() 上运动,若点
上运动,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)去九寨沟的概率为![]() ,不去泰山的概率为
,不去泰山的概率为![]() ;(2)所以
;(2)所以![]()
【解析】试题分析:
(1) 由题意列出所有可能的事件,结合古典概型公式可得小明去九寨沟的概率为![]() ,不去泰山的概率
,不去泰山的概率![]()
(2)由题意可得![]() ,结合圆的几何意义可得其最大值为
,结合圆的几何意义可得其最大值为![]() .
.
试题解析:
(1)由题意可知得到向量组合方式共有:
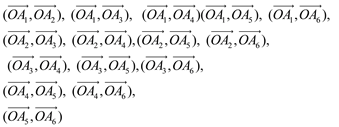
共15种
设事件“去九寨沟”=B,“不去泰山”=C
则去九寨沟即ξ>0: ![]()
共4种
![]()
去泰山即=0, ![]()
共4种
![]()
(2)由题意:小明去武夷山即![]()
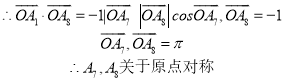
故可设![]()
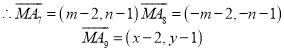
![]()
上式几何意义:圆![]() 上的点与点(6,3)的距离
上的点与点(6,3)的距离
上式的最大值即点![]()
距离的最大值,即圆心![]()
的距离再加半径
即![]()
所以![]()

练习册系列答案
相关题目
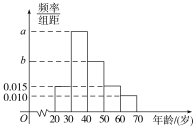
【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表:
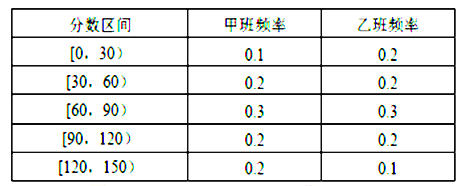
(1)若成绩120分以上(含120分)为优秀,求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(2)根据以上数据完成下面的![]() 列联表:在犯错概率小于
列联表:在犯错概率小于![]() 的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?
的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?

| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
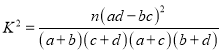 ,其中
,其中![]() .
.