题目内容
【题目】（本小题满分16分）已知
是虚数， 
是实数．
（1）求
为何值时， 
有最小值，并求出|
的最小值；
（2）设
，求证： 
为纯虚数．
【答案】（1）
（2）见解析
【解析】试题分析：（1）设
，化简
，利用
是虚数
为实数，解得
的轨迹方程，利用几何意义即可的结果；（2）根据（1）的结论化简
即可得结论.
试题解析：（1）设
，则
所以， 
，又
可得
表示点
到点
的距离，所以
最小值为
解方程组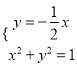
并结合图形得
（2）
又
，所以
为纯虚数
【 思路点晴】本题主要考查的是复数的乘法、除法运算和复数模的概念及复数的几何性质，属于难题题．解题时一定要注意
和运算的准确性，否则很容易出现错误．解本题的关键是先利用复数的模长公式列方程解出
的值，然后根据复数的乘法、除法的运算法则和
的性质化简
+
，最后再根据复数的几何意义求出
的范围. 
； 
， 
， 
， 
（
）．
练习册系列答案
相关题目
