题目内容
如图,设有双曲线 ,F1,F2是其两个焦点,点M在双曲线上.
,F1,F2是其两个焦点,点M在双曲线上.
(1)若∠F1MF2=90°,求△F1MF2的面积;
(2)若∠F1MF2=60°,△F1MF2的面积是多少?若∠F1MF2=120°,△F1MF2的面积又是多少?
(3)观察以上计算结果,你能看出随∠F1MF2的变化,△F1MF2的面积将怎样变化吗?试证明你的结论.

 ,F1,F2是其两个焦点,点M在双曲线上.
,F1,F2是其两个焦点,点M在双曲线上.(1)若∠F1MF2=90°,求△F1MF2的面积;
(2)若∠F1MF2=60°,△F1MF2的面积是多少?若∠F1MF2=120°,△F1MF2的面积又是多少?
(3)观察以上计算结果,你能看出随∠F1MF2的变化,△F1MF2的面积将怎样变化吗?试证明你的结论.

(1) 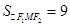 ; (2)
; (2) 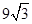 ,
,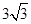 ; (3) θ增大时面积变小,证明过程见解析.
; (3) θ增大时面积变小,证明过程见解析.
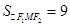 ; (2)
; (2) 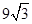 ,
,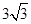 ; (3) θ增大时面积变小,证明过程见解析.
; (3) θ增大时面积变小,证明过程见解析.试题分析:(1) 设
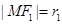 ,
,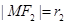 , 直角三角形△F1MF2中
, 直角三角形△F1MF2中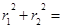
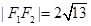 ,利用双曲线定义得
,利用双曲线定义得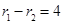 ,平方得
,平方得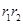 ,求得面积;(2) △F1MF2 中由余弦定理可得,|MF1|·|MF2|,由面积公式
,求得面积;(2) △F1MF2 中由余弦定理可得,|MF1|·|MF2|,由面积公式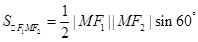 可得面积;(3) 由双曲线定义与余弦定理,可得面积与θ的关系
可得面积;(3) 由双曲线定义与余弦定理,可得面积与θ的关系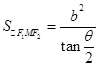 ,所以θ增大时面积变小.
,所以θ增大时面积变小.解:(1)由双曲线方程知a=2,b=3,
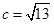 ,
,设
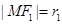 ,
,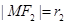 (
(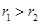 ).
).由双曲线定义,有
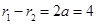 ,两边平方得,
,两边平方得,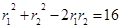 ,
,即
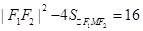 ,
,也即
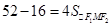 ,求得
,求得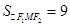 . 4分
. 4分(2)若∠F1MF2=60°,在△MF1F2中,
由余弦定理得
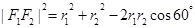 ,
,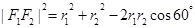 ,所以
,所以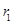
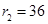 .
.求得
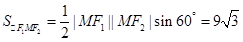 .
.同理可求得若∠F1MF2=120°,
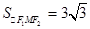 . 8分
. 8分(3)由以上结果猜想,随着∠F1MF2的增大,△F1MF2的面积将减小.
证明如下:
令∠F1MF2=θ,则
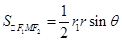 .
.由双曲线定义及余弦定理,有
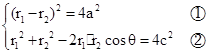
②-①得
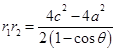 ,
,所以
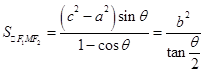 ,
,因为0<θ<π,
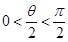 ,
,在
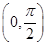 内,
内,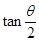 是增函数,
是增函数,因此当θ增大时,
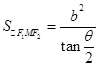 将减小. 12分
将减小. 12分
练习册系列答案
相关题目
 的左,右焦点分别为
的左,右焦点分别为 ,点P在双曲线的右支上,且
,点P在双曲线的右支上,且 ,则此双曲线的离心率e的最大值为 .
,则此双曲线的离心率e的最大值为 .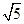 )2+y2=4,(x-
)2+y2=4,(x-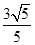 ,
,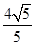 ),F(
),F(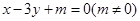 与双曲线
与双曲线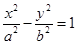 (
(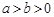 )两条渐近线分别交于点
)两条渐近线分别交于点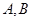 ,若点
,若点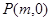 满足
满足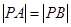 ,则该双曲线的离心率是__________
,则该双曲线的离心率是__________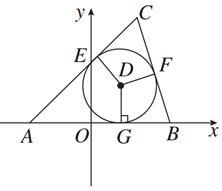
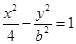 的右焦点与抛物线
的右焦点与抛物线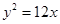 的焦点重合,则该双曲线的焦点到其渐近线的距离等于( ).
的焦点重合,则该双曲线的焦点到其渐近线的距离等于( ).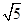
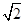
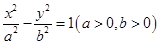 的离心率为
的离心率为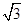 ,且直线
,且直线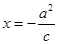 (c是双曲线的半焦距)与抛物线
(c是双曲线的半焦距)与抛物线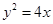 的准线重合,则此双曲线的方程为( )
的准线重合,则此双曲线的方程为( )



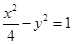 的离心率等于____________.
的离心率等于____________.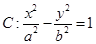
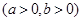 的顶点,B为双曲线C的虚轴一个端点.若△A1BA2是等边三角形,则双曲线
的顶点,B为双曲线C的虚轴一个端点.若△A1BA2是等边三角形,则双曲线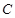 的离心率e等于 .
的离心率e等于 .