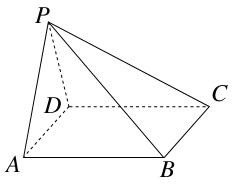
题目内容
(本小题满分14分)如图,在直三棱柱ABC-A1B1C1中,点D、E分别在边BC、
B1C1上,CD=B1E=AC,ÐA CD=60°.
CD=60°.
求证:(1)BE∥平面AC1D;
(2) 平面ADC1⊥平面BCC1B1.
平面ADC1⊥平面BCC1B1.
证明:(1)由三棱柱 是直三棱柱,得
是直三棱柱,得 .
.
因为点 分别边
分别边 上,
上, ,
,
所以 ,
, .
.
所以 四边形 是平行四形,所以
是平行四形,所以
因为 ,
,
所以 
(2)由三棱柱 是直三棱柱,得
是直三棱柱,得
因为 ,所以
,所以
在 中,由
中,由

得
所以
所以 ,即:
,即:
因为 ,
, ,
,
所以 
因为  所以
所以 
解析

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
已知点A(1,-2,11),B(4,2,3),C(6,-1,4),则△ABC的形状是( )
| A.锐角三角形 |
| B.钝角三角形 |
| C.直角三角形 |
| D.等边三角形 |
 中,底面
中,底面 是直角梯形,
是直角梯形, ,
, .
.
 平面
平面 ;
; ,使得
,使得 与平面
与平面 平行?证明你的结论.
平行?证明你的结论. 中,已知
中,已知 ,
, .
. ;
; 是
是 上一点,试确定
上一点,试确定 平面
平面 ,并证明.
,并证明.
 ,AA1=4,点D是AB的中点
,AA1=4,点D是AB的中点 AC⊥BC1;
AC⊥BC1; 的平面角的正切值.
的平面角的正切值.
 =
= =λ∈(0,1).
=λ∈(0,1).
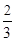 .
.
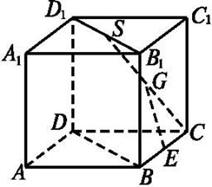
 中,
中, ,
, ,
, 为
为 上的点,且
上的点,且 ,
,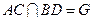 .
.
 平面
平面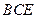 ;
;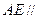 平面
平面 ;
; 的体积.
的体积.