题目内容
(本小题满分12)如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4, ,AA1=4,点D是AB的中点
,AA1=4,点D是AB的中点
(Ⅰ)求证: AC⊥BC1;
AC⊥BC1;
(Ⅱ)求二面角 的平面角的正切值.
的平面角的正切值.
(Ⅰ)证明:直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,
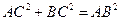
∴ AC⊥BC,  …………………1分
…………………1分
又 AC⊥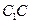 ,且
,且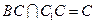
∴ AC⊥平面BCC1,又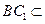 平面BCC1 ……………………………………3分
平面BCC1 ……………………………………3分
∴ AC⊥BC1 ………………………………………………………………4分
(Ⅱ)解法一:取 中点
中点 ,过
,过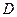 作
作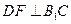 于
于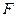 ,连接
,连接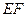 …………5分
…………5分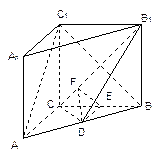
 是
是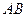 中点,
中点,
∴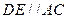 ,又
,又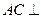 平面
平面
∴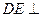 平面
平面 ,
,
又
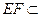 平面
平面 ,
,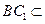 平面
平面
∴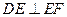
∴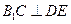 又
又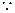
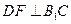 且
且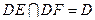
∴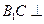 平面
平面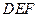 ,
,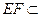 平面
平面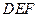 ………7分
………7分
∴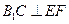 又
又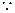
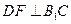
∴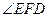 是二面角
是二面角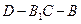 的平面角 ……………………………………8分
的平面角 ……………………………………8分 AC=3,BC=4,AA1=4,
AC=3,BC=4,AA1=4,
∴在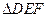 中,
中,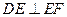 ,
, ,
,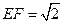
∴ …………………………………………11分
…………………………………………11分
∴二面角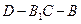 的正切值为
的正切值为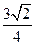 ………………………
……………………… …………………12分
…………………12分
解法二: 以
以 分别为
分别为 轴建立如图所示空间直角坐标系…………5分
轴建立如图所示空间直角坐标系…………5分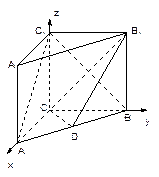
 AC=3,BC=4,AA1=4,
AC=3,BC=4,AA1=4,
∴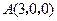 ,
,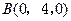
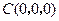 ,
,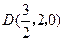 ,
,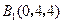 ,
,
∴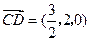 ,
,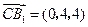
平面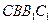 的法向量
的法向量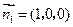 ,&n
,&n
解析

练习册系列答案
相关题目
已知 , 则
, 则 两点间距离的最小值是( )
两点间距离的最小值是( )
A. | B.2 | C. | D.1 |
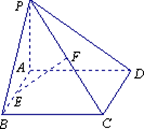
 中,底面
中,底面 是矩形,
是矩形, ,
, ,AB=2.M为PD的中点.求直线PC与平面ABM所成的角的正弦值;
,AB=2.M为PD的中点.求直线PC与平面ABM所成的角的正弦值;
 CD=60°.
CD=60°. 平面ADC1⊥平面BCC1B1.
平面ADC1⊥平面BCC1B1.

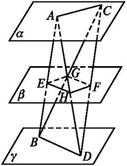
 B=2,BC=
B=2,BC=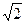 的矩形,侧面PAB
的矩形,侧面PAB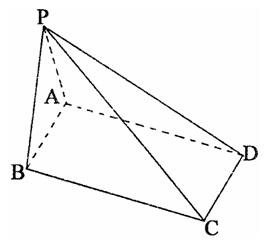
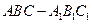 中,
中,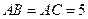 ,
,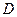 ,
,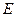 分别为
分别为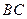 ,
,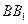 的中点,四边形
的中点,四边形 是边长为
是边长为 的正方形.
的正方形.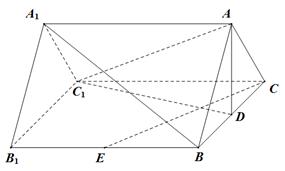
 ∥平面
∥平面 ;
;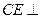 平面
平面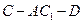 的余弦值.
的余弦值.