题目内容
正实数a、b满足a+3=b（a-1），则ab的最小值________．
9
分析：把已知a+3=b（a-1）变形为ab-3=a+b，再利用基本不等式的性质即可求出答案．
解答：∵正实数a、b满足a+3=b（a-1），∴ab-3=a+b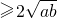
．当且仅当a=b时取等号．
令
，则t2-2t-3≥0，
∴（t-3）（t+2）≥0．
∵t＞0，∴t≥3，即
，∴ab≥9．
∴ab的最小值是9．
故答案为9．
点评：利用基本不等式的性质及换元是解题的关键．
分析：把已知a+3=b（a-1）变形为ab-3=a+b，再利用基本不等式的性质即可求出答案．
解答：∵正实数a、b满足a+3=b（a-1），∴ab-3=a+b
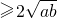．当且仅当a=b时取等号．令
，则t2-2t-3≥0，∴（t-3）（t+2）≥0．
∵t＞0，∴t≥3，即
，∴ab≥9．∴ab的最小值是9．
故答案为9．
点评：利用基本不等式的性质及换元是解题的关键．
练习册系列答案
相关题目
若正实数a，b满足a+b=1，则（ ）
A、
| ||||||
B、ab有最小值
| ||||||
C、
| ||||||
D、a2+b2有最小值
|