题目内容
某居民小区有两个相互独立的安全防范系统(简称系统)甲和乙,系统甲和系统乙在任意时刻发生故障的概率分别为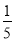 和
和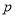 ,若在任意时刻至多有一个系统发生故障的概率为
,若在任意时刻至多有一个系统发生故障的概率为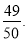
(Ⅰ)求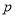 的值;
的值;
(Ⅱ)设系统乙在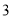 次相互独立的检测中不发生故障的次数为随机变量
次相互独立的检测中不发生故障的次数为随机变量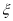 ,求
,求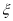 的数学期望
的数学期望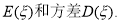
(Ⅰ) ;(Ⅱ)
;(Ⅱ)
【解析】
试题分析:(Ⅰ)根据在任意时刻至多有一个系统发生故障的概率为 ,根据对立事件的概率即:甲乙均不发生故障,进而求得关于
,根据对立事件的概率即:甲乙均不发生故障,进而求得关于 的值;(Ⅱ)
的值;(Ⅱ) 服从二项分布,根据二项分布的期望和方差公式,直接求得其期望和方差.
服从二项分布,根据二项分布的期望和方差公式,直接求得其期望和方差.
试题解析:(Ⅰ)记“系统甲发生故障、系统乙发生故障”分别为事件A、B,
“任意时刻至多有一个系统发生故障”为事件C。
则 ,
, 5分
5分
(Ⅱ)依题意 ,
, 8分
8分
 12分
12分
考点:1.对立事件的概率;2.二项分布的事件的期望和方差.

练习册系列答案
相关题目
 满足不等式组
满足不等式组 ,则
,则 的最大值为( )
的最大值为( ) ,则
,则 是
是 的
的 是偶函数,
是偶函数, 且当
且当 时,其导函数
时,其导函数 满足
满足 ,若
,若 ,则 B
,则 B



 ,
, ,全集
,全集 ,则
,则 ( )
( ) B.
B.
 D.
D.
 的最大值为 .
的最大值为 . 的图象沿
的图象沿 轴向右平移
轴向右平移 个单位后,得到一个偶函数的图象,则
个单位后,得到一个偶函数的图象,则 的取值不可能是( )
的取值不可能是( ) B.
B. C.
C. D.
D.
 是定义在
是定义在 上周期为
上周期为 的函数,且对任意的实数
的函数,且对任意的实数 ,恒有
,恒有 ,当
,当 ,
, .若
.若 在
在 有且仅有三个零点,则
有且仅有三个零点,则 的取值范围为( )
的取值范围为( ) B.
B. C.
C. D.
D.
 中,
中,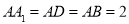 ,
,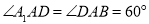 ,
, 是
是 的中点.
的中点.
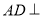 面
面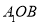 ;
;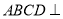 平面
平面 ,求
,求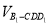 .
.