题目内容

若某几何体的三视图如图所示，则此几何体的体积是（　　）
A、6
B、
20
3
C、
22
3
D、
23
3
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由三视图可知：该几何体是一个正方体切去两个三棱锥所得的组合体，分别计算正方体和棱锥的体积，相减可得答案．
解答： 解：由三视图可知：该几何体是一个正方体切去两个三棱锥所得的组合体，如下图：

正方体的体积为：2×2×2=8，
三棱锥的体积为：
1
3
×（
1
2
×2×1）×2=
2
3
，
故组合体的体积V=8-2×
2
3
=
20
3
，
故选：B
点评：本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
已知函数F（x）=
f(x)
x
在定义域（0，+∞）内为单调增函数
（1）若f（x）=lnx+ax2，求a的取值范围
（2）设x0是f（x）的零点，m，n∈（0，x0），求证，
f(m+n)
f(m)+f(n)
＜1．
为了了解中学生的身体发育情况，对某中学17岁的60名女生的身高进行了测量，结果如下：154 159 166 169 159 156 166 162 158 167 156 166 160 164 160 157 151 157 161 162 158 153 158 164 158 163 158 153 157 163 162 159 154 165 166 157 151 146 157 158 160 165 158 163 163 162 161 154 165 159 162 159 157 159 149 164 168 159 153 160，根据数据列出样本的频率分布表，绘出频率直方图．
在平面直角坐标系xOy中，直线
x=a-t
y=t
（t为参数）与圆
x=1+cosθ
y=sinθ
（θ为参数）相切，切点在第一象限，则实数a的值为（　　）
A、
2
+1
B、
2
-1
C、1
D、
2
运行如图所示的程序框图后，输出的结果是
 
已知函数f（x）=x•ㄧxㄧ-2x．
（Ⅰ）求函数f（x）的零点；
（Ⅱ）画出y=f（x）的图象，并结合图象写出f（x）=m有三个不同实根时，实数m的取值范围；
（Ⅲ）写出函数f（x）的单调区间．
执行如图所示的程序框图，若输入x=-1，则输入y的值为（　　）
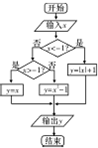
A、-1B、0C、1D、2
若函数f（x）=
x+3x，x≤0
1
3
x3-4x+
a
3
，x＞0
在其定义域上只有一个零点，则实数a的取值范围是（　　）
A、a＞16B、a≥16
C、a＜16D、a≤16
若函数y=sin（2x+θ）的图象向左平移
π
3
个单位后恰好与y=sin2x的图象重合，则θ的最小正值是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网