题目内容
已知{an}是等差数列,其前n项和为Sn,{bn}是等比数列,且a1=b1=2,a4+b4=27,S4-b4=10.
(1)求数列{an}与{bn}的通项公式;
(2)记Tn=anb1+an-1b2+…+a1bn,n∈N*,证明Tn+12=-2an+10bn(n∈N*).
解:(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q.由a1=b1=2,得a4=2+3d,b4=2q3,S4=8+6d.由条件,得方程组
 所以an=3n-1,bn=2n,n∈N*.
所以an=3n-1,bn=2n,n∈N*.
(2)证明:由(1)得
Tn=2an+22an-1+23an-2+…+2na1,①
2Tn=22an+23an-1+…+2na2+2n+1a1.②
由②-①,得
Tn=-2(3n-1)+3×22+3×23+…+3×2n+2n+2= +2n+2-6n+2=10×2n-6n-10.
+2n+2-6n+2=10×2n-6n-10.
而-2an+10bn-12=-2(3n -1)+10×2n-12=10×2n-6n-10,
故Tn+12=-2an+10bn,n∈N*.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 海里/时 B.34
海里/时 B.34 海里/时
海里/时 海里/时 D
海里/时 D .34
.34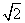 海里/时
海里/时 =( )
=( ) (n∈N+),设{an}的前n项和为Sn,则使Sn<-5成立的自然数n( )
(n∈N+),设{an}的前n项和为Sn,则使Sn<-5成立的自然数n( ) =
=
 ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn. 3)(n∈N+)成等差数列;命题q:数列
3)(n∈N+)成等差数列;命题q:数列 n,
n, ,3n(n∈N+)成等比数列.命题p是命题q的( )
,3n(n∈N+)成等比数列.命题p是命题q的( ) ≤9,则
≤9,则 的最大值是________.
的最大值是________. 表示的平面区域,并回答下列问题:
表示的平面区域,并回答下列问题: