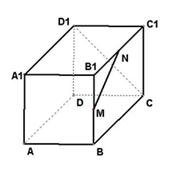
题目内容
如图,
已知正三棱柱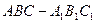 的底面边长是2,D是侧棱
的底面边长是2,D是侧棱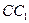 的中点,平面ABD和平面
的中点,平面ABD和平面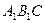 的交线为MN.
的交线为MN.
(Ⅰ)试证明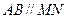 ;
;
(Ⅱ)若直线AD与侧面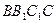 所成的角为
所成的角为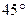 ,试求二面角
,试求二面角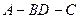 的大小.
的大小.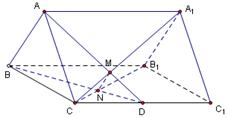
已知正三棱柱
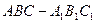 的底面边长是2,D是侧棱
的底面边长是2,D是侧棱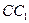 的中点,平面ABD和平面
的中点,平面ABD和平面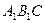 的交线为MN.
的交线为MN.(Ⅰ)试证明
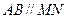 ;
;(Ⅱ)若直线AD与侧面
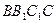 所成的角为
所成的角为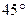 ,试求二面角
,试求二面角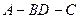 的大小.
的大小.
(Ⅰ)见解析 (Ⅱ)


(Ⅰ)由题意
 ,又
,又 ,
, ,
, 又
又 ,
, ,
, --------------------------------------------------4分
--------------------------------------------------4分(Ⅱ)取BC中点E,连AE,过E作
 于F,连AF.
于F,连AF. 是正三角形,
是正三角形, .
.又底面
 侧面
侧面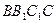 ,且交线为BC
,且交线为BC 侧面
侧面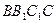
又



 为二面角
为二面角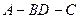 的平面角.--------------------7分
的平面角.--------------------7分连ED,则直线AD与侧面
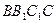 所成的角为
所成的角为 .
.设正三棱柱
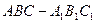 的侧棱长为
的侧棱长为 .则在
.则在 中,
中, 解得
解得 .
.  此正三棱柱的侧棱长为
此正三棱柱的侧棱长为 .
. --------------------------------------------------------9分
--------------------------------------------------------9分在
 中,
中, ,又
,又 ,
,  .
.又

 在
在 中,
中, . -----------------------------------------11分
. -----------------------------------------11分故二面角
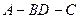 的大小为
的大小为 .
. 
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
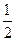 BD
BD
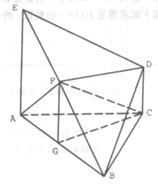
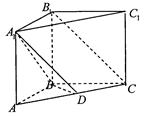
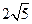 ,设这条最短路线与CC1的交
,设这条最短路线与CC1的交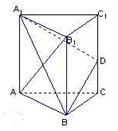
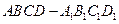 中,
中,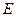 为
为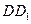 上的点、
上的点、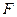 为
为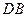 的中点.
的中点.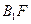 与平面
与平面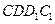 所成角的正弦值;
所成角的正弦值;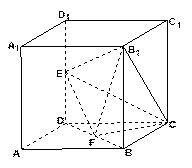 (Ⅱ)若直线
(Ⅱ)若直线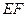 //平面
//平面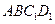 ,试确定点
,试确定点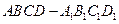 的棱
的棱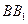 和
和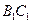 的中点,求:
的中点,求: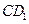 所成的角;
所成的角;