题目内容
设函数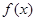 的定义域为
的定义域为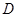 ,如果存在正实数
,如果存在正实数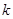 ,对于任意
,对于任意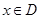 ,都有
,都有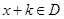 ,且
,且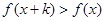 恒成立,则称函数
恒成立,则称函数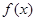 为
为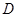 上的“
上的“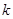 型增函数”,已知函数
型增函数”,已知函数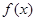 是定义在
是定义在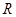 上的奇函数,且当
上的奇函数,且当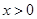 时,
时,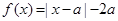 ,若
,若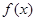 为
为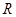 上的“2014型增函数”,则实数
上的“2014型增函数”,则实数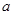 的取值范围是( )
的取值范围是( )
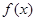 的定义域为
的定义域为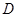 ,如果存在正实数
,如果存在正实数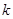 ,对于任意
,对于任意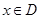 ,都有
,都有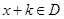 ,且
,且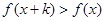 恒成立,则称函数
恒成立,则称函数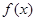 为
为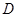 上的“
上的“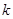 型增函数”,已知函数
型增函数”,已知函数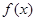 是定义在
是定义在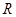 上的奇函数,且当
上的奇函数,且当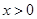 时,
时,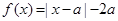 ,若
,若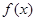 为
为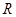 上的“2014型增函数”,则实数
上的“2014型增函数”,则实数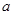 的取值范围是( )
的取值范围是( )A.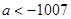 | B. | C.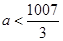 | D.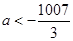 |
C
试题分析:
 是定义在
是定义在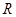 上的奇函数,
上的奇函数,
设
 ,则
,则 .
. ,
, .
.
 .
.①当
 时,由
时,由 ,可得
,可得 ,化为
,化为 ,由绝对值的几何意义可得
,由绝对值的几何意义可得 ,解得
,解得
②当
 时,由f(2014+x)>f(x),
时,由f(2014+x)>f(x),分为以下两类研究:当
 时,可得
时,可得 ,
,化为
 ,由绝对值的几何意义可得
,由绝对值的几何意义可得 ,解得
,解得 .
.当
 ,
, ,化为
,化为 ,
,故
 时成立.当
时成立.当 时,
时, ,
,③当
 时,由
时,由 可得
可得 ,当
,当 时成立,当
时成立,当 时,
时, .
.综上可知:
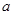 的取值范围是
的取值范围是 ,故选C.
,故选C.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
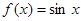 .
.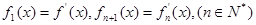 ,求
,求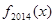 的解析式;
的解析式;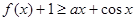 在
在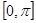 上恒成立,求实数
上恒成立,求实数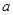 的取值范围.
的取值范围. 是
是 上以4为周期的可导偶函数,则曲线
上以4为周期的可导偶函数,则曲线 在
在 处的切线的斜率为()
处的切线的斜率为()


 是
是 上的奇函数,且
上的奇函数,且 ,下面关于
,下面关于 ;
; 对称;
对称; 对称.
对称.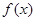 满足
满足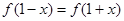 ,且在
,且在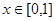 时,
时,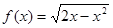 ,若直线
,若直线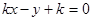
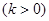 与函数
与函数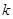 的取值范围是( )
的取值范围是( )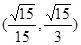
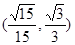
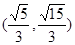
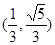
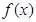 ,以下四个命题中错误的是 ( )
,以下四个命题中错误的是 ( )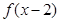 的图象关于点A(2,0)对称
的图象关于点A(2,0)对称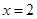 对称,则
对称,则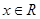 ,有
,有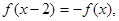 则4是
则4是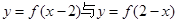 的图象关于直线
的图象关于直线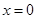 对称
对称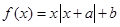 是奇函数的充要条件是
是奇函数的充要条件是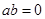
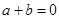
 ;
; ;
;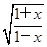 ;
;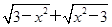 .
.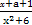 为奇函数,则实数a= .
为奇函数,则实数a= .