题目内容
8.函数f(x)=x3的图象关于( )对称.| A. | y轴 | B. | 直线y=x | C. | 坐标原点 | D. | 直线y=-x |
分析 确定函数f(x)=x3是奇函数,可得函数f(x)=x3的图象关于坐标原点对称.
解答 解:∵f(-x)=(-x)3=-x3=-f(x),
∴函数f(x)=x3是奇函数,
∴函数f(x)=x3的图象关于坐标原点对称.
故选:C.
点评 本题考查函数图象的对称性,确定函数f(x)=x3是奇函数是关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
16.已知函数f(x)=sinx+acosx的图象的一条对称轴是$x=\frac{π}{4}$,若不等式asin2x+cosx-t≥0对$x∈[-\frac{π}{3},\frac{π}{2}]$恒成立,则t的取值范围是( )
| A. | (-∞,1] | B. | (-∞,2] | C. | (1,+∞) | D. | (0,1) |
3.若函数f(x)=x3-2mx+m3在定义域上单调递增,则( )
| A. | m≥0 | B. | m<0 | C. | m≤0 | D. | m≤$\frac{3}{2}$ |
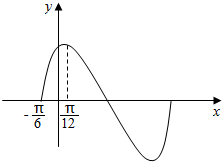 如图是函数f(x)=2sinωx•cosωx+2$\sqrt{3}$cos2ωx-$\sqrt{3}$(ω>0)的一部分图象.
如图是函数f(x)=2sinωx•cosωx+2$\sqrt{3}$cos2ωx-$\sqrt{3}$(ω>0)的一部分图象.