题目内容
18.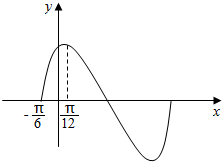 如图是函数f(x)=2sinωx•cosωx+2$\sqrt{3}$cos2ωx-$\sqrt{3}$(ω>0)的一部分图象.
如图是函数f(x)=2sinωx•cosωx+2$\sqrt{3}$cos2ωx-$\sqrt{3}$(ω>0)的一部分图象.(1)求ω的值;
(2)在△ABC中,已知a=3,b+c=6,求f(A-$\frac{π}{3}$)的最大值.
分析 (1)化简可得f(x)=2sin(2ωx+$\frac{π}{3}$),由图象可得周期,由周期公式可得ω=1;
(2)由已知式子和基本不等式可得bc≤9,再由余弦定理可得cosA≥$\frac{1}{2}$,可得0<A≤$\frac{π}{3}$,而f(A-$\frac{π}{3}$)=2sin(2A-$\frac{π}{3}$),由三角函数的最值可得.
解答 解:(1)化简可得f(x)=2sin•c+2$\sqrt{3}$cos2ωx-$\sqrt{3}$
=sin2ωx+$\sqrt{3}$cos2ωx=2sin(2ωx+$\frac{π}{3}$),
由图象可知周期T满足$\frac{T}{4}$=$\frac{π}{12}$-(-$\frac{π}{6}$),∴T=π,
∴$\frac{2π}{2ω}$=π,解得ω=1;
(2)∵a=3,b+c=6,∴36=(b+c)2=b2+c2+2bc≥4bc,
∴bc≤9,由余弦定理可得cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{bc}$=$\frac{36-2bc-9}{2bc}$=$\frac{27}{2bc}$-1≥$\frac{1}{2}$,
∴0<A≤$\frac{π}{3}$,∴f(A-$\frac{π}{3}$)=2sin[2(A-$\frac{π}{3}$)+$\frac{π}{3}$)]=2sin(2A-$\frac{π}{3}$),
由0<A≤$\frac{π}{3}$可得-$\frac{π}{3}$<2A-$\frac{π}{3}$≤$\frac{π}{3}$,故当2A-$\frac{π}{3}$=$\frac{π}{3}$时,f(A-$\frac{π}{3}$)取最大值$\sqrt{3}$
点评 本题考查三角函数的最值,涉及三角函数的周期性和余弦定理以及基本不等式,属中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题是“若x≠1,则x2-3x+2≠0” | |
| B. | “x=1”是“x2-3x+2=0”的充分不必要条件 | |
| C. | 对于命题p:?x∈R可使x2+x+1<0,则?p为:?x∈R,均有x2+x+1≥0 | |
| D. | 若命题p且q为假命题,则p、q均为假命题 |
| A. | y轴 | B. | 直线y=x | C. | 坐标原点 | D. | 直线y=-x |