题目内容
函数f(x)= (a为常数)在(-2,2)内为增函数,则实数a的取值范围是________.
(a为常数)在(-2,2)内为增函数,则实数a的取值范围是________.
a
分析:首先对已知函数进行化简,分离常数a,根据函数f(x)在(-2,2)内为增函数判断出a的取值范围.
解答:∵f(x)= (a为常数),
(a为常数),
 =
= =a+
=a+
∵f(x)在(-2,2)内为增函数,而y=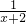 为减函数
为减函数
∴要使f(x)在(-2,2)内为增函数
∴-2a+1<0
解得:a>
故答案为:a> ;
;
点评:本题考查函数单调性的应用,通过对函数的分析,判断各部分的单调性,是一道基础题.

分析:首先对已知函数进行化简,分离常数a,根据函数f(x)在(-2,2)内为增函数判断出a的取值范围.
解答:∵f(x)=
 (a为常数),
(a为常数), =
= =a+
=a+
∵f(x)在(-2,2)内为增函数,而y=
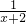 为减函数
为减函数∴要使f(x)在(-2,2)内为增函数
∴-2a+1<0
解得:a>

故答案为:a>
 ;
;点评:本题考查函数单调性的应用,通过对函数的分析,判断各部分的单调性,是一道基础题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 =(2cosx,2sinx),
=(2cosx,2sinx), =
= ,函数f(x)=
,函数f(x)= •
• ,
, (a为常数).
(a为常数). 成立,当且仅当x1=x2时取“=”.求证:当
成立,当且仅当x1=x2时取“=”.求证:当 时,函数g(x)在(-∞,+∞)上是增函数.
时,函数g(x)在(-∞,+∞)上是增函数. ,其中a为常数,e为自然对数的底数.
,其中a为常数,e为自然对数的底数. ,其中a为实数.
,其中a为实数. 恒成立?若不存在,请说明理由,若在,求出a的值并加以证明.
恒成立?若不存在,请说明理由,若在,求出a的值并加以证明.