题目内容
(本小题满分14分)
已知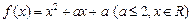 ,
,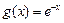 ,
,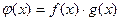 .
.
(Ⅰ)当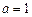 时,求
时,求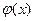 的单调区间;
的单调区间;
(Ⅱ)求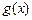 在点
在点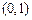 处的切线与直线
处的切线与直线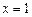 及曲线
及曲线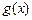 所围成的封闭图形的面积;
所围成的封闭图形的面积;
(Ⅲ)是否存在实数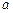 ,使
,使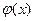 的极大值为3?若存在,求出
的极大值为3?若存在,求出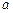 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
已知
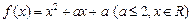 ,
,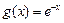 ,
,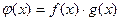 .
.(Ⅰ)当
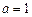 时,求
时,求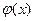 的单调区间;
的单调区间;(Ⅱ)求
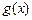 在点
在点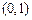 处的切线与直线
处的切线与直线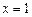 及曲线
及曲线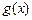 所围成的封闭图形的面积;
所围成的封闭图形的面积;(Ⅲ)是否存在实数
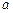 ,使
,使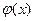 的极大值为3?若存在,求出
的极大值为3?若存在,求出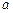 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.解:(1)当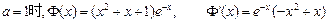 .…(1分)
.…(1分)
 ……(3分)
……(3分)
∴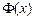 的单调递增区间为(0,1),
的单调递增区间为(0,1),
单调递减区间为: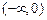 ,
,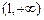 . ……(4分)
. ……(4分)
(2)切线的斜率为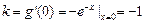 ,
,
∴切线方程为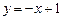 .……(6分)
.……(6分)
所求封闭图形面积为
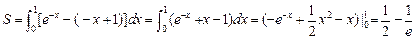 . ……(8分)
. ……(8分)
(3)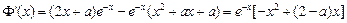 , ……(9分)
, ……(9分)
令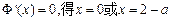 . ……(10分)
. ……(10分)
若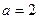 ,
,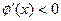 ,则
,则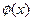 在R上单调递减,不存在极大值,舍去;
在R上单调递减,不存在极大值,舍去;
若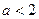
列表如下:
由表可知,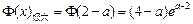 . ……(12分)
. ……(12分)
设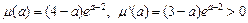 ,
,
∴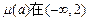 上是增函数,……(13分)
上是增函数,……(13分)
∴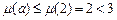 ,即
,即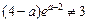 ,
,
∴不存在实数a,使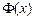 极大值为3. ……(14分)
极大值为3. ……(14分)
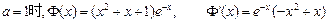 .…(1分)
.…(1分) ……(3分)
……(3分)∴
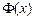 的单调递增区间为(0,1),
的单调递增区间为(0,1),单调递减区间为:
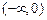 ,
,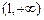 . ……(4分)
. ……(4分)(2)切线的斜率为
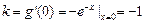 ,
,∴切线方程为
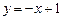 .……(6分)
.……(6分)所求封闭图形面积为
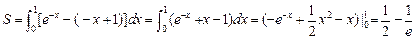 . ……(8分)
. ……(8分)(3)
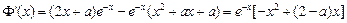 , ……(9分)
, ……(9分)令
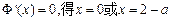 . ……(10分)
. ……(10分)若
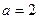 ,
,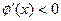 ,则
,则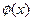 在R上单调递减,不存在极大值,舍去;
在R上单调递减,不存在极大值,舍去;若
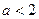
列表如下:
| x | (-∞,0) | 0 | (0,2-a) | 2-a | (2-a,+ ∞) |
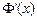 | - | 0 | + | 0 | - |
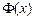 | ↘ | 极小 | ↗ | 极大 | ↘ |
由表可知,
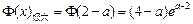 . ……(12分)
. ……(12分)设
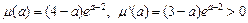 ,
,∴
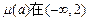 上是增函数,……(13分)
上是增函数,……(13分)∴
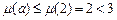 ,即
,即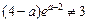 ,
,∴不存在实数a,使
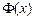 极大值为3. ……(14分)
极大值为3. ……(14分)略

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
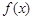 是奇函数,且当
是奇函数,且当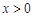 时,
时,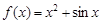 ,则当
,则当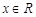 时,
时,

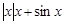

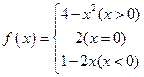 ,
,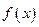 图像;
图像;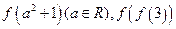 的值;
的值;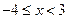 时,求
时,求 ,则
,则



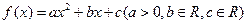 ,若函数
,若函数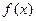 的最小值是
的最小值是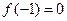 ,且
,且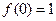 ,对称轴是
,对称轴是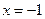 ,
,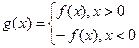 .
.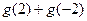 的值;
的值;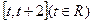 上的最小值.
上的最小值.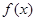 的定义域为
的定义域为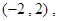 导函数为
导函数为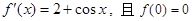 ,则满足
,则满足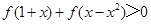 的实数
的实数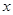 的取值范围为
的取值范围为 



 所过定点的横、纵坐标分别是等差数列
所过定点的横、纵坐标分别是等差数列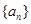 的第二项与第三项,若
的第二项与第三项,若 ,数列
,数列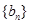 的前
的前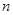 项和为
项和为 ,则
,则 =( )
=( )


 ,
, 。
。 ;
; 的解集;
的解集; 时,求函数
时,求函数 的最大值。
的最大值。 的定义域是
的定义域是