题目内容
14.已知函数f(x)=$\frac{a+lnx}{x}$在点(1,f(1))处的切线与x轴平行.(1)若函数f(x)在区间(m,m+1)上存在极值,求实数m的取值范围;
(2)求证:当x>1时,$\frac{1}{e+1}$•(x+1)•f(x)>$\frac{2}{e+1}$>$\frac{2{e}^{x-1}}{x{e}^{x}+1}$.
分析 (1)求得函数的导数,求得切线的斜率,解方程可得a=1,求出极值点,可得m<1<m+1,可得m的范围;
(2)要证$\frac{1}{e+1}$•(x+1)•f(x)>$\frac{2}{e+1}$,即证(x+1)(1+lnx)>2x,在x>1成立.可令g(x)=(x+1)(1+lnx)-2x,x>1,求得导数,判断单调性,即可得证;要证$\frac{2}{e+1}$>$\frac{2{e}^{x-1}}{x{e}^{x}+1}$,即证ex-1(e+1)-xex-1<0,x>1.可设h(x)=ex-1(e+1)-xex-1,x>1,求出导数,判断单调性,即可得证.
解答 解:(1)函数f(x)=$\frac{a+lnx}{x}$的导数为f′(x)=$\frac{1-a-lnx}{{x}^{2}}$,
由在点(1,f(1))处的切线与x轴平行,可得1-a=0,
即有a=1,则f(x)=$\frac{1+lnx}{x}$,
即有f′(x)=$\frac{-lnx}{{x}^{2}}$,由f′(x)=0,可得x=1,
且x=1为极大值点,
由函数f(x)在区间(m,m+1)上存在极值,可得m<1<m+1,
即有0<m<1:
(2)证明:$\frac{1}{e+1}$•(x+1)•f(x)-$\frac{2}{e+1}$=$\frac{1}{e+1}$[(x+1)•$\frac{1+lnx}{x}$-2].
要证$\frac{1}{e+1}$•(x+1)•f(x)>$\frac{2}{e+1}$,
即证(x+1)(1+lnx)>2x,在x>1成立.
可令g(x)=(x+1)(1+lnx)-2x,x>1,
g′(x)=1+lnx+(x+1)•$\frac{1}{x}$-2=1+lnx+$\frac{x-1}{x}$>0,
即有g(x)在(1,+∞)递增,则g(x)>g(1)=0,
则有$\frac{1}{e+1}$•(x+1)•f(x)>$\frac{2}{e+1}$;
要证$\frac{2}{e+1}$>$\frac{2{e}^{x-1}}{x{e}^{x}+1}$,即证ex-1(e+1)-xex-1<0,x>1.
可设h(x)=ex-1(e+1)-xex-1,x>1,
h′(x)=ex-1(e+1)-xex-ex=ex($\frac{1}{e}$-x)<0,
即有h(x)在(1,+∞)递减,即h(x)<h(1)=0,
则$\frac{2}{e+1}$>$\frac{2{e}^{x-1}}{x{e}^{x}+1}$.
综上可得,当x>1时,$\frac{1}{e+1}$•(x+1)•f(x)>$\frac{2}{e+1}$>$\frac{2{e}^{x-1}}{x{e}^{x}+1}$.
点评 本题考查导数的运用:求切线的斜率和极值,考查不等式的证明,注意运用构造函数法,由导数的符号判断单调性,考查运算和推理能力,属于中档题.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案| A. | y=|x| | B. | y=lnx | C. | y=x${\;}^{\frac{1}{3}}$ | D. | y=x-3 |
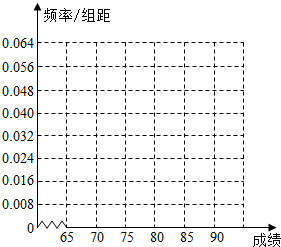 在党的群众教育路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对本单位的各项开展工作进行打分评价,现获得如下的数据:70,82,81,76,84,80,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,74,86,79,76,根据上述数据得到样本的频率分布表如下:
在党的群众教育路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对本单位的各项开展工作进行打分评价,现获得如下的数据:70,82,81,76,84,80,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,74,86,79,76,根据上述数据得到样本的频率分布表如下:(1)根据上述数据完成样本的频率分布表;
(2)根据(1)频率分布表,完成样本频率分布直方图;
(3)根据样本频率分布直方图,以频率作为概率,求在该单位中任取6名员工的打分,他们的打分在(75,85]内的人员数X的数学期望.
| 分组 | 频数 | 频率 |
| [65,70] | ||
| (70,75] | ||
| (75,80] | ||
| (80,85] | ||
| (85,90] |
| A. | 40° | B. | 50° | C. | 90° | D. | 150° |
 已知:⊙O的方程为x2+y2=9,点A(5,0),过点A作⊙O的切线AP,P为切点.
已知:⊙O的方程为x2+y2=9,点A(5,0),过点A作⊙O的切线AP,P为切点.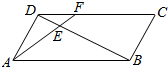 如图,点E是平行四边形ABCD对角线BD的n(n∈N且n≥2)等分点中最靠近点D的那点.线段AE的延长线交CD于点F,若向量$\overrightarrow{AF}=\frac{1}{n-1}\overrightarrow{AB}+x\overrightarrow{AD}$,则实数x的值为1.
如图,点E是平行四边形ABCD对角线BD的n(n∈N且n≥2)等分点中最靠近点D的那点.线段AE的延长线交CD于点F,若向量$\overrightarrow{AF}=\frac{1}{n-1}\overrightarrow{AB}+x\overrightarrow{AD}$,则实数x的值为1.