题目内容
4.定义在(0,+∞)上的函数f(x),满足f(mn)=f(m)+f(n)(m,n>0),且当x>1时,f(x)>0.(1)求f(1)的值;
(2)求证:f($\frac{m}{n}$)=f(m)-f(n)
分析 (1)利用特殊值法令令m=n=1,可得f(1)=f(1)+f(1),求出f(1)的值;
(2)对f(m)进行变形可得f(m)=f($\frac{m}{n}$n),利用题中条件可得f(m)=f($\frac{m}{n}$n)=f($\frac{m}{n}$)+f(n),得出结论.
解答 解:(1)令m=n=1
∴f(1)=f(1)+f(1)
∴f(1)=0;
证明(2)f(m)=f($\frac{m}{n}$×n)
=f($\frac{m}{n}$)+f(n)
∴f($\frac{m}{n}$)=f(m)-f(n)
点评 考察了抽象函数的求值问题和对条件的利用.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
12.已知点A(0,2),抛物线C:y2=2px(p>0)的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,若$\frac{|FM|}{|MN|}=\frac{{\sqrt{5}}}{5}$,则p的值等于( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | 2 | D. | 4 |
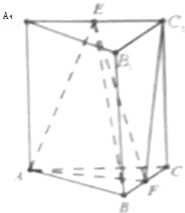 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,E,F分别为A1C1,BC的中点,AA1=3,AC=2,BC=1,AB⊥BC.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,E,F分别为A1C1,BC的中点,AA1=3,AC=2,BC=1,AB⊥BC.