题目内容
【题目】已知函数![]() (
(![]() 为常数,
为常数, ![]() 为自然对数的底数),曲线
为自然对数的底数),曲线![]() 在与
在与![]() 轴的交点
轴的交点![]() 处的切线斜率为-1.
处的切线斜率为-1.
(1)求![]() 的值及函数
的值及函数![]() 的单调区间;
的单调区间;
(2)证明:当![]() 时,
时, ![]() ;
;
(3)证明:当![]() 时,
时, 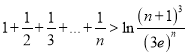 .
.
【答案】(1)![]() ,
, ![]() 在区间
在区间![]() 上单调递减,在
上单调递减,在![]() 上单调递增;(2)证明见解析;(3)证明见解析.
上单调递增;(2)证明见解析;(3)证明见解析.
【解析】试题分析:(1)求出函数的f′(x)=ex﹣a.通过f′(x)=ex﹣2>0,即可求解函数f(x)在区间(﹣∞,ln2)上单调递减,在(ln2,+∞)上单调递增.
(2)求出f(x)的最小值,化简f(x)≥1﹣ln4.构造g(x)=ex﹣x2﹣1,通过g′(x)>0.判断g(x)在(0,+∞)上单调递增,得到g(x)>g(0),推出结果.
(3)首先证明:当x>0时,恒有![]() .令
.令![]() ,则h′(x)=ex﹣x2.推出h(x)在(0,+∞)上单调递增,得到x+ln3>3lnx.利用累加法推出
,则h′(x)=ex﹣x2.推出h(x)在(0,+∞)上单调递增,得到x+ln3>3lnx.利用累加法推出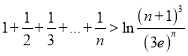 .
.
试题解析:
(1)由![]() ,得
,得![]() .
.
又![]() ,所以
,所以![]() .所以
.所以![]() ,
, ![]() .
.
由![]() ,得
,得![]() .
.
所以函数![]() 在区间
在区间![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)证明:由(1)知![]() .
.
所以![]() ,即
,即![]() ,
, ![]() .
.
令![]() ,则
,则![]() .
.
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,即
,即![]() .
.
(3)首先证明:当![]() 时,恒有
时,恒有![]() .
.
证明如下:令![]() ,则
,则![]() .
.
由(2)知,当![]() 时,
时, ![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,所以
,所以![]() .所以
.所以![]() ,即
,即![]() .依次取
.依次取![]() ,代入上式,则
,代入上式,则![]() ,
, ![]() ,
, ![]()
![]() .
.
以上各式相加,有![]() .
.
所以![]() ,
,
所以, ![]()
即![]() .
.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目