题目内容
在△ABC中，若（a+b+c）（a-b+c）=3ac，且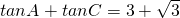
，AB边上的高为
，求角A，B，C的大小与边a，b，c的长．
解：（a+b+c）（a-b+c）=3ac，a2+c2-b2=ac，cosB=
tan（A+C）=
，tanAtanC=2+
，联合tanA+tanC=3+
得
，即
当A=75°，C=45°时，b=
-1），a=8
当A=45°，C=75°时，b=
+1），a=8
∴当A=75°，B=60°，C=45°时，a=8，b=4（3
-1），
当A=45°，B=60°，C=75°时，a=8，b=4
+1）．
分析：利用余弦定理，结合（a+b+c）（a-b+c）=3ac可求B，利用和角的正切公式，结合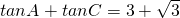可求A、C，再利用正弦定理求边．
点评：本题主要考查利用正弦、余弦定理解决三角形问题，正确利用公式是关键．
tan（A+C）=
，tanAtanC=2+，联合tanA+tanC=3+得
，即当A=75°，C=45°时，b=
-1），a=8当A=45°，C=75°时，b=
+1），a=8∴当A=75°，B=60°，C=45°时，a=8，b=4（3
-1），当A=45°，B=60°，C=75°时，a=8，b=4
+1）．分析：利用余弦定理，结合（a+b+c）（a-b+c）=3ac可求B，利用和角的正切公式，结合
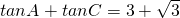可求A、C，再利用正弦定理求边．点评：本题主要考查利用正弦、余弦定理解决三角形问题，正确利用公式是关键．
练习册系列答案
轻松暑假总复习系列答案
相关题目
在△ABC中，若
=
，
=
，
=
且
•
=
•
=
•
，则△ABC的形状是△ABC的（ ）
| BC |
| a |
| CA |
| b |
| AB |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
| A、锐角三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
如图，在△ABC中，若在△ABC中，若（a+b+c）（b+c-a）=3bc，且sinA=2sinBcosC，则△ABC的形状是（ ）
| A、直角三角形 | B、等腰直角三角形 | C、等腰三角形 | D、等边三角形 |