题目内容
19.已知M(-1,0),F(1,0),动点P满足$\overrightarrow{MP}•\overrightarrow{MF}=2|{\overrightarrow{FP}}|$,过F的直线交P的轨迹C于A,B两点,若AB的垂直平分线经过点Q(0,5),求直线AB的斜率.分析 利用动点P满足$\overrightarrow{MP}•\overrightarrow{MF}=2|{\overrightarrow{FP}}|$,建立方程,化简,求动点P的轨迹C的方程,设AB的方程为y=k(x-1),代入y2=4x,求出AB的中点坐标,利用AB的垂直平分线经过点Q(0,5),求直线AB的斜率.
解答 解:设P(x,y),则$\overrightarrow{MP}$=(x+1,y),$\overrightarrow{FP}$=(x-1,y),$\overrightarrow{MF}$=(2,0),
∵$\overrightarrow{MP}•\overrightarrow{MF}=2|{\overrightarrow{FP}}|$,
∴2(x+1)=2$\sqrt{(x-1)^{2}+{y}^{2}}$,
∴y2=4x;
设AB的方程为y=k(x-1),代入y2=4x,可得k2x2-(2k2+4)x+k2=0,
∴AB的中点坐标为(1+$\frac{2}{{k}^{2}}$,$\frac{2}{k}$),
∵AB的垂直平分线经过点Q(0,5),
∴AB的垂直平分线的斜率为$\frac{\frac{2}{k}-5}{1+\frac{2}{{k}^{2}}}$,
∴$\frac{\frac{2}{k}-5}{1+\frac{2}{{k}^{2}}}$•k=-1,
∴k=1,即直线AB的斜率是1.
点评 本题考查轨迹方程,考查直线与抛物线的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
9.设点O(0,0,0),A(2,-1,3),B(-1,4,-2),C(3,1,λ),若O,A,B,C四点共面,则实数λ等于( )
| A. | $\frac{26}{7}$ | B. | $\frac{27}{7}$ | C. | 4 | D. | $\frac{29}{7}$ |
7.函数f(x)=6-x-x2的单调递减区间是( )
| A. | $[-\frac{1}{2},+∞)$ | B. | $[-\frac{1}{2},2)$ | C. | $(-∞,-\frac{1}{2}]$ | D. | (-3,$-\frac{1}{2}]$ |
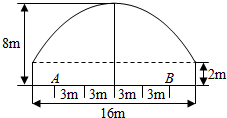 有一隧道,内设双行线公路,同方向有两个车道(共有四个车道),每个车道宽为3m,此隧道的截面由一个长方形和一抛物线构成.如图所示,隧道高8m,宽16m,为了保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方面上高度之差至少为0.25m,靠近中轴线的车道为快车道,两侧的车道为慢车道,求车辆通过隧道时,慢车道的限制高度(用分数表示).
有一隧道,内设双行线公路,同方向有两个车道(共有四个车道),每个车道宽为3m,此隧道的截面由一个长方形和一抛物线构成.如图所示,隧道高8m,宽16m,为了保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方面上高度之差至少为0.25m,靠近中轴线的车道为快车道,两侧的车道为慢车道,求车辆通过隧道时,慢车道的限制高度(用分数表示).