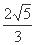题目内容
设函数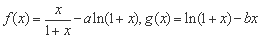 .
.
(1)若函数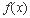 在
在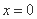 处有极值,求函数
处有极值,求函数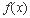 的最大值;
的最大值;
(2)①是否存在实数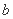 ,使得关于
,使得关于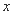 的不等式
的不等式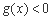 在
在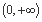 上恒成立?若存在,求出
上恒成立?若存在,求出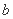 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
②证明:不等式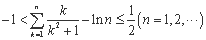
(1)由已知得: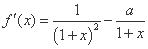 ,且函数
,且函数 在
在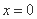 处有极值
处有极值
∴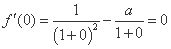 ,即
,即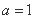 ∴
∴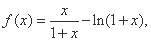
∴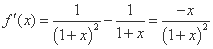
当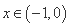 时,
时,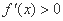 ,
, 单调递增;
单调递增;
当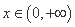 时,
时,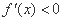 ,
, 单调递减;
单调递减;
∴函数 的最大值为
的最大值为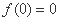
(2)①由已知得: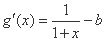
(i)若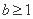 ,则
,则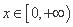 时,
时,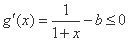
∴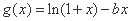 在
在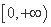 上为减函数,
上为减函数,
∴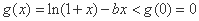 在
在 上恒成立;
上恒成立;
(ii)若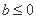 ,则
,则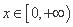 时,
时,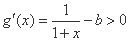
∴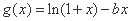 在
在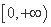 上为增函数,
上为增函数,
∴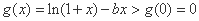 ,不能使
,不能使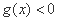 在
在 上恒成立;
上恒成立;
(iii)若 ,则
,则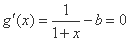 时,
时,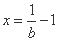 ,
,
当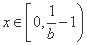 时,
时,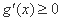 ,∴
,∴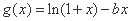 在
在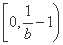 上为增函数,
上为增函数,
此时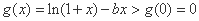 ,
,
∴不能使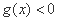 在
在 上恒成立;
上恒成立;
综上所述,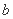 的取值范围是
的取值范围是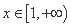
②由以上得: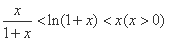
取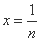 得:
得: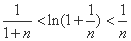
令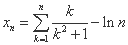 ,
,
则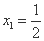 ,
,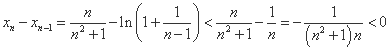 .
.
因此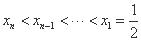 .
.
又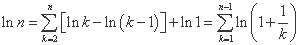
故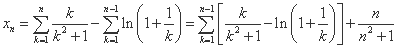

练习册系列答案
相关题目

 在
在 上的最大值和最小值,并求出对应的
上的最大值和最小值,并求出对应的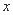 值.
值. 中,角
中,角 的对边分别为
的对边分别为 .若
.若 ,
, ,求实数
,求实数 的最小值.
的最小值. 的导函数是
的导函数是 =___________.
=___________.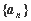 中,已知
中,已知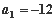 ,
,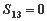 ,使得
,使得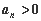 的最小正整数n为
的最小正整数n为 的右支上,线段BC的垂直平分线DA交y轴于点
的右支上,线段BC的垂直平分线DA交y轴于点 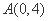 ,若
,若 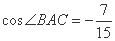 ,则点A到直线BC的距离d=____.
,则点A到直线BC的距离d=____.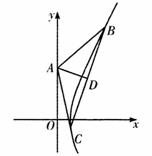

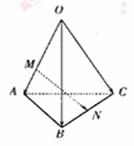
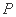 在正方体
在正方体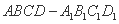 的面对角线
的面对角线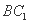 上运动,则下列四个命题:
上运动,则下列四个命题: 的体积不变; ②
的体积不变; ②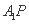 ∥平面
∥平面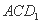 ;
;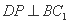 ; ④平面
; ④平面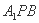 ⊥平面
⊥平面 .
.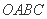 中,
中,
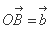
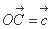 ,点
,点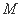 在
在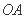 上,且
上,且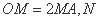 是
是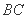 的中点,则
的中点,则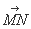 等于( )
等于( )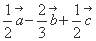 B.
B.
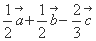 D.
D.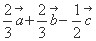
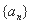 满足
满足 ,若存在两项
,若存在两项 使得
使得 ,则
,则 的最小值为 ( )
的最小值为 ( )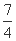 B、
B、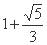 C、
C、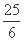 D、
D、