题目内容
已知正项等比数列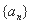 满足
满足 ,若存在两项
,若存在两项 使得
使得 ,则
,则 的最小值为 ( )
的最小值为 ( )
A 、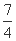 B、
B、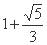 C、
C、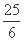 D、
D、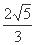
A

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
已知正项等比数列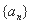 满足
满足 ,若存在两项
,若存在两项 使得
使得 ,则
,则 的最小值为 ( )
的最小值为 ( )
A 、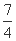 B、
B、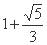 C、
C、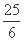 D、
D、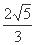
A

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案