题目内容
已知单位向量
,
,它们的夹角为60°,若
=2
+(t-1)
,
⊥
,则t的值为 .
| a |
| b |
| c |
| a |
| b |
| c |
| b |
考点:数量积表示两个向量的夹角,平面向量数量积的运算
专题:计算题,平面向量及应用
分析:由单位向量的定义与向量数量积的公式,算出
•
=
.根据
⊥
,得
•
=0即[2
+(t-1)
]•
=0,化简整理得到关于t的方程,解之即可得到实数t的值.
| a |
| b |
| 1 |
| 2 |
| c |
| b |
| c |
| b |
| a |
| b |
| b |
解答:
解:∵向量
、
是单位向量,
∴|
|=|
|=1,
2=|
|2=1.
∵
、
的夹角为60°,
∴
•
=|
|•|
|cos60°=
.
又∵
=2
+(t-1)
,
⊥
,
∴
•
=[2
+(t-1)
]•
=0,
即2
•
+(t-1)
2=0,
可得2×
+(t-1)×1=0,
解得t=0.
故答案为:0
| a |
| b |
∴|
| a |
| b |
| b |
| b |
∵
| a |
| b |
∴
| a |
| b |
| a |
| b |
| 1 |
| 2 |
又∵
| c |
| a |
| b |
| c |
| b |
∴
| c |
| b |
| a |
| b |
| b |
即2
| a |
| b |
| b |
可得2×
| 1 |
| 2 |
解得t=0.
故答案为:0
点评:本题给出单位向量满足的条件,在
⊥
的情况下求实数t的值,着重考查了单位向量的定义、向量垂直的条件、向量的数量积及其运算性质等知识,属于中档题.
| c |
| b |

练习册系列答案
相关题目
不等式x-2y+5>0表示的区域在直线x-2y+5=0的( )
| A、右上方 | B、右下方 |
| C、左上方 | D、左下方 |
设a=50.3,b=0.35,c=log50.3+log52,则a,b,c的大小关系是( )
| A、b<c<a |
| B、a<b<c |
| C、c<a<b |
| D、c<b<a |
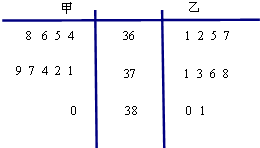 学校为了预防甲流感,每天上午都要对同学进行体温抽查.某一天,随机抽取甲、乙两个班级各10名同学,测量他们的体温如图:(单位0.1℃)
学校为了预防甲流感,每天上午都要对同学进行体温抽查.某一天,随机抽取甲、乙两个班级各10名同学,测量他们的体温如图:(单位0.1℃)