题目内容
6.设△ABC的内角A、B、C所对边的长分别为a、b、c,已知a=5,b+c=2a,3sinA=5sinB,则角C的大小是$\frac{2π}{3}$.分析 由正弦定理化简已知等式可得3a=5b,进而可求b,c的值,利用余弦定理可求cosC的值,结合范围C∈(0,π),即可得解C的值.
解答 解:∵3sinA=5sinB,
∴由正弦定理可得:3a=5b,
又∵a=5,b+c=2a,
∴b=3,c=7,
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{{5}^{2}+{3}^{2}-{7}^{2}}{2×5×3}$=-$\frac{1}{2}$,
又∵C∈(0,π),
∴C=$\frac{2π}{3}$.
故答案为:$\frac{2π}{3}$.
点评 本题主要考查了正弦定理,余弦定理在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
18.设M为边长为4的正方形ABCD的边BC的中点,N为正方形区域内任意一点(含边界),则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最大值为( )
| A. | 32 | B. | 24 | C. | 20 | D. | 16 |
15.若集合A={x|x2+3x-4>0},B={x|-2<x≤3},且M=A∩B,则有( )
| A. | 1∈M | B. | 2∈M | C. | (∁RB)⊆A | D. | B⊆A |
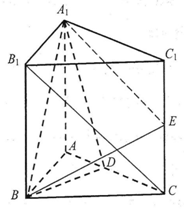 如图,侧棱垂直于底面的三棱柱ABC-A1B1C1中,D,E分别是AC,CC1的中点,$AB=BC=A{A_1}=\frac{{\sqrt{2}}}{2}AC$.
如图,侧棱垂直于底面的三棱柱ABC-A1B1C1中,D,E分别是AC,CC1的中点,$AB=BC=A{A_1}=\frac{{\sqrt{2}}}{2}AC$.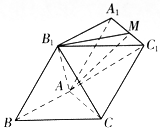 如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,且侧面ABB1A1⊥底面ABC.
如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,且侧面ABB1A1⊥底面ABC.