题目内容
设函数f(x)=
是奇函数(a、b、c∈Z),且f(1)=2,f(2)<3.
(1)求a、b、c的值;
(2)判断并证明f(x)在[1,+∞]上的单调性.
| ax2+1 |
| bx+c |
(1)求a、b、c的值;
(2)判断并证明f(x)在[1,+∞]上的单调性.
考点:函数单调性的判断与证明,函数解析式的求解及常用方法
专题:常规题型
分析:先由函数f(x)=
是奇函数确定整数a,b,c的值,再通过定义法证明函数的单调性.
| ax2+1 |
| bx+c |
解答:
解:(1)由题意得,
解得a=1,b=1,c=0.
(2)f(x)在[1,+∞)上单调递增,证明如下:
任取x1,x2∈[1,+∞);且x1<x2,则
f(x1)-f(x2)=
-
=
∵1≤x1<x2,
∴x1x2-1>0,x1-x2<0,x1x2>0
∴f(x1)-f(x2)<0
∴f(x)在[1,+∞)上单调递增.
|
(2)f(x)在[1,+∞)上单调递增,证明如下:
任取x1,x2∈[1,+∞);且x1<x2,则
f(x1)-f(x2)=
| ||
| x1 |
| ||
| x2 |
=
| (x1x2-1)(x1-x2) |
| x1x2 |
∵1≤x1<x2,
∴x1x2-1>0,x1-x2<0,x1x2>0
∴f(x1)-f(x2)<0
∴f(x)在[1,+∞)上单调递增.
点评:本题考查了利用函数的奇偶性求参数的方法,及函数的单调性的判断与证明.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
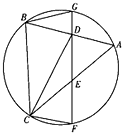 如图,D,E分别是△ABC的边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,BG=BD.
如图,D,E分别是△ABC的边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,BG=BD. 如图空间四边形ABCD,E、F、G、H分别为AB、AD、CB、CD的中点且AC=BD,AC⊥BD,试判断四边形EFGH的形状,并证明.
如图空间四边形ABCD,E、F、G、H分别为AB、AD、CB、CD的中点且AC=BD,AC⊥BD,试判断四边形EFGH的形状,并证明.