题目内容
20.方程$\sqrt{1-{x}^{2}}$=k(x-1)+2有两个不等实根,则k的取值范围是( )| A. | ($\frac{3}{4}$,+∞) | B. | ($\frac{1}{3}$,1] | C. | (0,$\frac{3}{4}$) | D. | ($\frac{3}{4}$,1] |
分析 由题意可得,函数y=$\sqrt{1-{x}^{2}}$的图象和直线y=k(x-1)+2有2个交点,数形结合求得k的范围.
解答 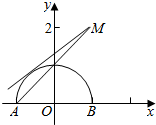 解:方程$\sqrt{1-{x}^{2}}$=k(x-1)+2有两个不等实根,
解:方程$\sqrt{1-{x}^{2}}$=k(x-1)+2有两个不等实根,
即函数y=$\sqrt{1-{x}^{2}}$的图象和直线y=k(x-1)+2有2个交点.
而函数y=$\sqrt{1-{x}^{2}}$的图象是以原点为圆心,半径等于1的上半圆
(位于x轴及x轴上方的部分),
直线y=k(x-1)+2,即kx-y+2-k=0 的斜率为k,且经过点M(1,2),
当直线和半圆相切时,由$\frac{|0+0+2-k|}{\sqrt{1+{k}^{2}}}$=1,求得k=$\frac{3}{4}$.
当直线经过点A(-1,0)时,由0=k(-1-2)+3求得k=1.
数形结合可得k的范围为($\frac{3}{4}$,1],
故选:D.
点评 本题主要考查方程的根的存在性及个数判断,体现了函数和方程的转化及数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
10.下列三句话按三段论的模式排列顺序正确的是( )
①Z1,Z2不能比较大小;②Z1,Z2是虚数;③虚数不能比较大小.
①Z1,Z2不能比较大小;②Z1,Z2是虚数;③虚数不能比较大小.
| A. | ①②③ | B. | ②①③ | C. | ②③① | D. | ③②① |
11.已知集合A={x|x≥2},B={x|1≤x≤3},则A∩B=( )
| A. | {x|-1<x≤3} | B. | {x|2≤x≤3} | C. | {x|x=3} | D. | ∅ |
15.下列命题中的假命题是( )
| A. | ?x∈R,2-x+1>1 | B. | ?x∈[1,2],x2-1≥0 | ||
| C. | ?x∈R,sinx+cosx=2 | D. | ?x∈R,${x^2}+\frac{1}{{{x^2}+1}}≤1$ |
5.正四面体的四个面上分别写有数字0,1,2,3,把两个这样的四面体抛在桌面上,露在外面的6个数字为2,0,1,3,0,3的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{64}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{16}$ |