题目内容
若等比数列{an}前n项和为Sn=2n+a,则复数z=
在复平面上对应的点位于( )
| i |
| a+i |
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
∵等比数列{an}前n项和为Sn=2n+a,
∴a1=2+a,
a2=(4+a)-(2+a)=2,
a3=(8+a)-(4+a)=4,
∴22=(2+a)×4,
解得a=-1.
∴z=
=
=
=
=
-
i,
∴复数z=
在复平面上对应的点(
,-
)位于第四象限.
故选D.
∴a1=2+a,
a2=(4+a)-(2+a)=2,
a3=(8+a)-(4+a)=4,
∴22=(2+a)×4,
解得a=-1.
∴z=
| i |
| a+i |
| i |
| -1+i |
| i(-1-i) |
| (-1-i)(-1+i) |
| 1-i |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴复数z=
| i |
| a+i |
| 1 |
| 2 |
| 1 |
| 2 |
故选D.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
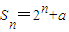 ,则复数z=
,则复数z= 在复平面上对应的点位于( )
在复平面上对应的点位于( )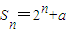 ,则复数z=
,则复数z=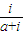 在复平面上对应的点位于( )
在复平面上对应的点位于( )