题目内容
若等比数列{an}前n项和为Sn=-2n+a,则复数z=
在复平面上对应的点位于( )
| i |
| a+i |
分析:由等比数列{an}前n项和求前三项,再由等比数列的定义求得a的值,利用两个复数代数形式的乘除法,化简复数z,求得它在复平面内对应点的坐标,从而得出结论.
解答:解:等比数列{an}前n项和为Sn=-2n+a,则此等比数列的前三项分别为 S1=a-2,S2-S1=-2,S3-S2=-4.
由22=(a-2)(-4),求得a=3.
故复数z=
=
=
=
,它在复平面内对应点的坐标为(
,
),
故选A.
由22=(a-2)(-4),求得a=3.
故复数z=
| i |
| a+i |
| i |
| 3+i |
| i(3-i) |
| (3+i)(3-i) |
| 1+3i |
| 10 |
| 1 |
| 10 |
| 3 |
| 10 |
故选A.
点评:本题主要考查由等比数列{an}前n项和求前几项的方法,等比数列的定义,两个复数代数形式的乘除法,虚数单位i的幂运算性质,复数与复平面内对应点之间的关系,属于基础题.

练习册系列答案
相关题目
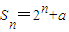 ,则复数z=
,则复数z= 在复平面上对应的点位于( )
在复平面上对应的点位于( )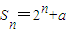 ,则复数z=
,则复数z=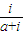 在复平面上对应的点位于( )
在复平面上对应的点位于( )