题目内容
已知函数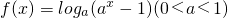
（Ⅰ）求f（x）的定义域；
（Ⅱ） 讨论f（x）的单调性；
（Ⅲ） 解不等式f（2x）＞f-1（x）．
解：（Ⅰ）由题意，ax＞1=a0，因为0＜a＜1，所以x＜0，
即f（x）的定义域为{x|x＜0}…（2分）
（Ⅱ）函数f（x）在（-∞，0）上是单调递增的．…（4分）
令函数u（x）=ax-1，
因为0＜a＜1
所以u（x）=ax-1在（-∞，0）上是单调递减的，
又因为g（x）=logax也是单调递减的，
由复合函数的单调性知，
复合函数f（x）=g（u（x））在（-∞，0）上是单调递增的．…（8分）
（Ⅲ）由题知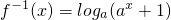
，x∈R…（10分）
于是不等式f（2x）＞f-1（x）等价为a2x-1＜ax+1即：（ax-2）（ax+1）＜0
从而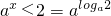
，所以x＞loga2，又须2x＜0，
综上，原不等式的解集为{x|loga2＜x＜0}…（12分）
分析：（Ⅰ）对数函数的定义域为真数大于0，由此可求f（x）的定义域；
（Ⅱ）令函数u（x）=ax-1，从而可知u（x）=ax-1在（-∞，0）上是单调递减的，又因为g（x）=logax也是单调递减的，由复合函数的单调性，可得f（x）的单调性．…（8分）
（Ⅲ）由题知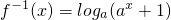，从而不等式f（2x）＞f-1（x）等价为a2x-1＜ax+1，从而可求不等式的解集．
点评：本题以对数函数为载体，考查对数函数的定义域，考查复合函数的单调性，同时考查不等式的解法，考查学生等价转化问题的能力．
即f（x）的定义域为{x|x＜0}…（2分）
（Ⅱ）函数f（x）在（-∞，0）上是单调递增的．…（4分）
令函数u（x）=ax-1，
因为0＜a＜1
所以u（x）=ax-1在（-∞，0）上是单调递减的，
又因为g（x）=logax也是单调递减的，
由复合函数的单调性知，
复合函数f（x）=g（u（x））在（-∞，0）上是单调递增的．…（8分）
（Ⅲ）由题知
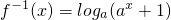，x∈R…（10分）于是不等式f（2x）＞f-1（x）等价为a2x-1＜ax+1即：（ax-2）（ax+1）＜0
从而
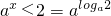，所以x＞loga2，又须2x＜0，综上，原不等式的解集为{x|loga2＜x＜0}…（12分）
分析：（Ⅰ）对数函数的定义域为真数大于0，由此可求f（x）的定义域；
（Ⅱ）令函数u（x）=ax-1，从而可知u（x）=ax-1在（-∞，0）上是单调递减的，又因为g（x）=logax也是单调递减的，由复合函数的单调性，可得f（x）的单调性．…（8分）
（Ⅲ）由题知
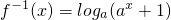，从而不等式f（2x）＞f-1（x）等价为a2x-1＜ax+1，从而可求不等式的解集．点评：本题以对数函数为载体，考查对数函数的定义域，考查复合函数的单调性，同时考查不等式的解法，考查学生等价转化问题的能力．
练习册系列答案
相关题目
．
．
上的最大值和最小值．
．
，求f（α）．
．
上的最大值和最小值．