题目内容
已知函数f(x)=x2+ax+2 在[-5,5]上为单调函数,求实数a的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:先求出函数的对称轴,结合函数的单调性,从而得到a的范围.
解答:
解:∵函数的对称轴是x=-
,开口向上,
若f(x)在[-5,5]递增,则-
≤-5,即a≥10,
若f(x)在[-5,5]递减,则-
≥-5,即a≤-10,
∴a的范围是(-∞,-10]∪[10,+∞).
| a |
| 2 |
若f(x)在[-5,5]递增,则-
| a |
| 2 |
若f(x)在[-5,5]递减,则-
| a |
| 2 |
∴a的范围是(-∞,-10]∪[10,+∞).
点评:本题考查了二次函数的性质,考查了函数的单调性,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
化简
等于( )
| 3+cos6-2sin23 |
| A、-2cos3 |
| B、2cos3 |
| C、4cos3 |
| D、sin3 |
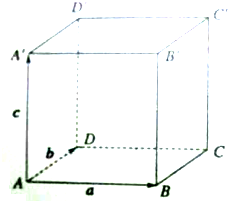 已知正方体ABCD-A′B′C′D′的棱长为1,设
已知正方体ABCD-A′B′C′D′的棱长为1,设