题目内容
各项均为正数的数列{an}中,设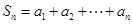 ,
, ,且
,且 ,
,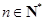 .
.
(1)设 ,证明数列{bn}是等比数列;
,证明数列{bn}是等比数列;
(2)设 ,求集合
,求集合 .
.
(1)详见解析,(2)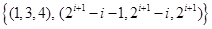 (
(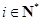 ).
).
解析试题分析:(1)数列{bn}是等比数列,实际就是证明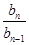 为常数,首先列出
为常数,首先列出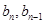 的关系式,由
的关系式,由 知消去参数
知消去参数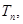 由
由 ,所以
,所以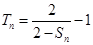 ①,当
①,当 时,
时, ②,①-②,得
②,①-②,得 即
即 ,
,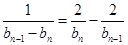 ,化简得
,化简得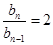 或
或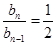 (
( ).因为数列{an}的各项均为正数,所以数列
).因为数列{an}的各项均为正数,所以数列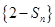 单调递减,所以
单调递减,所以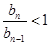 .所以
.所以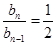 (
( ).
).
(2)由(1)知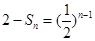 ,所以
,所以 ,即
,即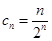 .由
.由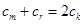 ,得
,得 ,又
,又 时,
时,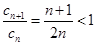 ,所以数列
,所以数列 从第2项开始依次递减.当
从第2项开始依次递减.当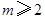 时,若
时,若 ,则
,则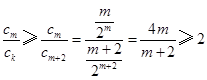 ,与
,与 矛盾,所以
矛盾,所以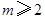 时,
时,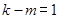 ,即
,即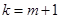 .令
.令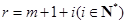 ,则
,则 ,所以
,所以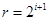 ,即存在满足题设的数组
,即存在满足题设的数组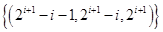 (
(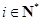 ).当
).当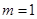 时,若
时,若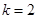 ,则
,则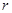 不存在;若
不存在;若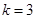 ,则
,则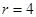 ;若
;若 时,
时, ,(*)式不成立.
,(*)式不成立.
【解】(1)当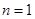 时,
时,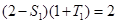 ,
,
即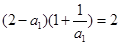 ,解得
,解得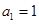 . 2分
. 2分
由 ,所以
,所以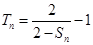 ①
①
当 时,
时, ②
②
①-②,得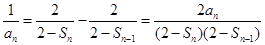 (
( ), 4分
), 4分
即 ,
,
即 ,所以
,所以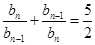 ,
,
因为数列{an}的各项均为正数,所以数列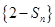 单调递减,所以
单调递减,所以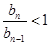 .
.
所以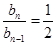 (
( ).
).
因为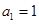 ,所以
,所以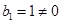 ,
,
所以数列{bn}是等比数列. 6分
(2)由(1)知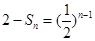 ,所以
,所以

练习册系列答案
相关题目
 中,若
中,若 且
且 ,则数列
,则数列 ____________。
____________。 前
前 项和
项和 ,
,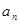 ;(2)若它的第
;(2)若它的第 项满足
项满足 ,求
,求 ,an=
,an= (
(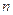 为正整数),
为正整数), ,cn=(an+19)(Sn+50),数列{cn}前n项和为Tn,
,cn=(an+19)(Sn+50),数列{cn}前n项和为Tn, 的首项
的首项 ,公差
,公差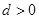 ,且第
,且第 项、第
项、第 项、第
项、第 项分别是等比数列
项分别是等比数列 的第
的第 项、第
项、第 项.
项. 对任意
对任意 ,均有
,均有 成立.
成立. ; ②求
; ②求 .
. 满足
满足 (
( ).
). 的值;
的值; (用含
(用含 的式子表示);
的式子表示); ,求
,求 为等差数列,
为等差数列, ,其前n项和为
,其前n项和为 ,若
,若 ,
, 值.
值. ,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值. 的前n项和为
的前n项和为 ,已知
,已知 ,
, 是
是 和
和 的等比中项.
的等比中项.