题目内容
7.若数列{an}中,a1=$\frac{1}{3}$,an+1=$\frac{n+1}{3n}$an(Ⅰ)证明:{$\frac{{a}_{n}}{n}$}是等比数列,并求{an}的通项公式;
(Ⅱ)若{an}的前n项和为Sn,求证Sn$<\frac{3}{4}$.
分析 (Ⅰ)由题意可得$\frac{{a}_{n+1}}{n+1}$=$\frac{1}{3}$•$\frac{{a}_{n}}{n}$,结合等比数列的定义,即可得证,再由等比数列的通项公式即可求得{an}的通项公式;
(Ⅱ)运用错位相减法,结合等比数列的求和公式,化简整理可得Sn,再由不等式的性质即可得证.
解答 (Ⅰ)证明:a1=$\frac{1}{3}$,an+1=$\frac{n+1}{3n}$an
即有$\frac{{a}_{n+1}}{n+1}$=$\frac{1}{3}$•$\frac{{a}_{n}}{n}$,
则{$\frac{{a}_{n}}{n}$}是首项为$\frac{1}{3}$,公比为$\frac{1}{3}$的等比数列,
即有$\frac{{a}_{n}}{n}$=($\frac{1}{3}$)n,
即an=n•($\frac{1}{3}$)n;
(Ⅱ)证明:{an}的前n项和为Sn,
即有Sn=1•$\frac{1}{3}$+2•($\frac{1}{3}$)2+3•($\frac{1}{3}$)3+…+n•($\frac{1}{3}$)n,
$\frac{1}{3}$Sn=1•($\frac{1}{3}$)2+2•($\frac{1}{3}$)3+3•($\frac{1}{3}$)4+…+n•($\frac{1}{3}$)n+1,
两式相减可得,$\frac{2}{3}$Sn=$\frac{1}{3}$+($\frac{1}{3}$)2+($\frac{1}{3}$)3+…+($\frac{1}{3}$)n-n•($\frac{1}{3}$)n+1,
=$\frac{\frac{1}{3}(1-\frac{1}{{3}^{n}})}{1-\frac{1}{3}}$-n•($\frac{1}{3}$)n+1,
化简可得Sn=$\frac{3}{4}$-$\frac{1}{4•{3}^{n-1}}$-$\frac{n}{2•{3}^{n}}$<$\frac{3}{4}$.
则Sn$<\frac{3}{4}$.
点评 本题考查等比数列的定义的运用,考查数列的通项公式的求法,同时考查数列的求和方法:错位相减法,以及等比数列的求和公式的运用,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 8个 | B. | 6个 | C. | 4个 | D. | 2个 |
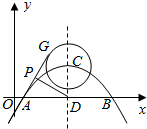 已知抛物线$y=-\frac{3}{16}(x-1)(x-9)$与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,⊙C的半径为2,G为⊙C上一动点,P为AG的中点,则DP的最大值为( )
已知抛物线$y=-\frac{3}{16}(x-1)(x-9)$与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,⊙C的半径为2,G为⊙C上一动点,P为AG的中点,则DP的最大值为( )| A. | $\frac{7}{2}$ | B. | $\frac{{\sqrt{41}}}{2}$ | C. | $\frac{{\sqrt{34}}}{2}$ | D. | $2\sqrt{3}$ |
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |