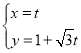��Ŀ����
����Ŀ�������ͱ�Ğ��bienao���ǡ������������̹������������ij�ν.��ͼ��ʾ��ȡһ�������壬����ͼб��һ��Ϊ����������ģһ��������������Ϊǵ�£���ͼ��.��������һ��ǵ�µ�һ����������Ե����ʿ�����������������һ������һ������洹ֱ��������Ϊ����������![]() ������������Ϊ��Ğ������
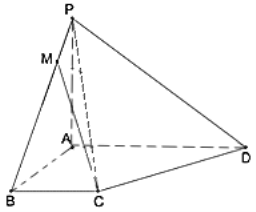
������������Ϊ��Ğ������![]() ������ij�������������и���õ�һ������һ����Ğ���Ҹ�����������ͼ�ͱ�Ğ�IJ���ͼ��ͼ��ʾ���������������ͱ�Ğ�ı����֮��Ϊ�� ��
������ij�������������и���õ�һ������һ����Ğ���Ҹ�����������ͼ�ͱ�Ğ�IJ���ͼ��ͼ��ʾ���������������ͱ�Ğ�ı����֮��Ϊ�� ��

A.![]() B.
B.![]()
C.![]() D.
D.![]()
���𰸡�B
��������
���ȸ�������ͼ�õ��������������ⳤ���ټ�������������.
�������ͼ��֪��
��������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
���������ı����![]()
![]() .
.
�ڱ�Ğ�У�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
���Ա�Ğ�ı����![]()
![]()
![]() ��
��
���������ͱ�Ğ�ı����֮��![]()
![]() .
.
��ѡ��B

����Ŀ��ij���������µ꿪ҵ������ٰ�һ��ʳƷ���ᣬ�д����Ϲ˿��Գ�.��Ŀ����ͨ���������![]() ��ʳƷ����λ�����
��ʳƷ����λ�����![]() �����ˣ����������ԭ��������
�����ˣ����������ԭ��������![]() ���������õ�����ͳ�Ʊ���
���������õ�����ͳ�Ʊ���
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | |
�λ����������ˣ� |
|
|
|
|
|
ԭ���ϣ����� |
|
|
|
|
|
��1����������![]() �����ݣ����
�����ݣ����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��
��2����֪����ԭ���ϵķ���![]() ��Ԫ��������
��Ԫ��������![]() �������Ĺ�ϵΪ
�������Ĺ�ϵΪ![]() ��Ͷ��ʹ�õ�ÿ��ԭ������Ӧ����������Ϊ
��Ͷ��ʹ�õ�ÿ��ԭ������Ӧ����������Ϊ![]() Ԫ�������ԭ����ֻ������������Ϥ���ν��״���Լ��
Ԫ�������ԭ����ֻ������������Ϥ���ν��״���Լ��![]() ���˲μӣ����ݣ�1������������Իع鷽�̣�Ԥ�����Ӧ������ٴ�ԭ���ϣ����ܻ�����������������Ƕ��٣���ע������
���˲μӣ����ݣ�1������������Իع鷽�̣�Ԥ�����Ӧ������ٴ�ԭ���ϣ����ܻ�����������������Ƕ��٣���ע������![]() ��������
��������![]() ԭ���Ϸ��ã�.
ԭ���Ϸ��ã�.
�ο���ʽ�� ��
��![]() .
.
�ο����ݣ�![]() ��
��![]() ��
��![]() .
.