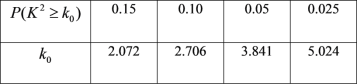题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为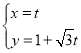 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() (2)
(2)![]()
【解析】
(1)消去参数可得直线的普通方程,利用极坐标与直角坐标的转化公式可得曲线C的直角坐标方程;
(2)联立直线的参数方程和曲线的直角坐标方程,结合直线参数方程的几何意义和韦达定理即可求得![]() 的值.
的值.
(1)![]() 直线
直线![]() 的参数方程为
的参数方程为 ,(t为参数)
,(t为参数)
∴消去参数![]() 后,直线
后,直线![]() 的普通方程为
的普通方程为![]() ,
,
![]() 的极坐标方程为
的极坐标方程为![]() ,
,
∴![]() ,∴
,∴![]() ,
,
整理得,曲线C的普通方程为![]() .
.
(2)设![]() 两点对应的参数分别为
两点对应的参数分别为![]() ,
,
将直线![]() 方程
方程 (t为参数),代入曲线C:
(t为参数),代入曲线C:![]() ,
,
得,![]() ,
,
∴![]() ,
,
∴![]() =
= .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】独立性检验中,假设![]() :运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得
:运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得![]() 的观测值
的观测值![]() .下列结论正确的是( )
.下列结论正确的是( )
附:
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
A. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动有关
B. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动无关
C. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动有关
D. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动无关