题目内容
已知f(x)=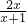 ,则f(
,则f( )+f(
)+f(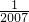 )+…+f(
)+…+f( )+f(1)+f(2)+…+f(2008)=______.
)+f(1)+f(2)+…+f(2008)=______.
解:由于f(x)=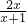 ,则f(
,则f( )=
)=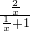 =
= ,∴f(x)+f(
,∴f(x)+f( )=2.
)=2.
∴f( )+f(
)+f(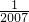 )+…+f(
)+…+f( )+f(1)+f(2)+…+f(2008)
)+f(1)+f(2)+…+f(2008)
=[f( )+f(2008)]+[f(
)+f(2008)]+[f(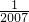 )+f(2007)]+…+[f(
)+f(2007)]+…+[f( )+f(2)]+f(1)
)+f(2)]+f(1)
=2007×2+1=4015,
故答案为 4015.
分析:由题意可得 f(x)+f( )=2,故要求的式子为[f(
)=2,故要求的式子为[f( )+f(2008)]+[f(
)+f(2008)]+[f(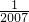 )+f(2007)]+…+[f(
)+f(2007)]+…+[f( )+f(2)]+f(1),运算求得结果.
)+f(2)]+f(1),运算求得结果.
点评:本题主要考查求函数的值的方法,求得f(x)+f( )=2,是解题的关键,属于基础题.
)=2,是解题的关键,属于基础题.
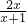 ,则f(
,则f( )=
)=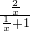 =
= ,∴f(x)+f(
,∴f(x)+f( )=2.
)=2.∴f(
 )+f(
)+f(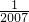 )+…+f(
)+…+f( )+f(1)+f(2)+…+f(2008)
)+f(1)+f(2)+…+f(2008)=[f(
 )+f(2008)]+[f(
)+f(2008)]+[f(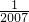 )+f(2007)]+…+[f(
)+f(2007)]+…+[f( )+f(2)]+f(1)
)+f(2)]+f(1)=2007×2+1=4015,
故答案为 4015.
分析:由题意可得 f(x)+f(
 )=2,故要求的式子为[f(
)=2,故要求的式子为[f( )+f(2008)]+[f(
)+f(2008)]+[f(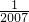 )+f(2007)]+…+[f(
)+f(2007)]+…+[f( )+f(2)]+f(1),运算求得结果.
)+f(2)]+f(1),运算求得结果.点评:本题主要考查求函数的值的方法,求得f(x)+f(
 )=2,是解题的关键,属于基础题.
)=2,是解题的关键,属于基础题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目