题目内容
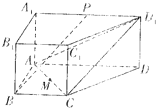 在棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是直角梯形,∠ABC=∠BAD=90°,AD=2AB=2BC=4,P是A1D1的中点.
在棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是直角梯形,∠ABC=∠BAD=90°,AD=2AB=2BC=4,P是A1D1的中点.(1)求证:BP∥平面ACD1;
(2)若M是AC的中点,且B1M⊥平面ACD1,求线段BB1的长.
分析:(1)由题意可得:PD1=BC,结合题意可得:PD1∥BC,PD1=BC,所以四边形BCD1P为平行四边形,即可根据线面平行的判定定理可证明线面平行.
(2)连接D1M,B1D1,BM,B1M,由线面垂直可得B1M⊥D1M,所以B1M2+D1M2=B1D12.同理可得:B1B⊥BM.设B1B=x,则B1M2=x2+2.在Rt△ABC中,可求得在Rt△B1A1D1中,可得B1D1=2
,所以x2+2+10+x2=20,即可求出x的值,进而求出答案.
(2)连接D1M,B1D1,BM,B1M,由线面垂直可得B1M⊥D1M,所以B1M2+D1M2=B1D12.同理可得:B1B⊥BM.设B1B=x,则B1M2=x2+2.在Rt△ABC中,可求得在Rt△B1A1D1中,可得B1D1=2
| 5 |
解答:解:(1)证明:因为P为A1D1的中点,
所以PD1=
A1D1=
AD=BC.
又因为底面ABCD是直角梯形,∠ABC=∠BAD=90°,
所以AD∥BC∥A1D1,
即PD1∥BC,PD1=BC,
所以四边形BCD1P为平行四边形.
所以BP∥CD1,
又因为BP不在平面ACD1内,
所以BP∥平面ACD1.
(2)连接D1M,B1D1,BM,B1M,
因为B1M⊥平面ACD1,
所以B1M⊥D1M,
所以B1M2+D1M2=B1D12.
又因为B1B⊥平面ABCD,
所以B1B⊥BM.
设B1B=x,由AB=BC=2可得BM=
,则B1M2=x2+2.
在Rt△ABC中,可求得DM=
,
所以D1M2=10+x2.
在Rt△B1A1D1中,可得B1D1=2
,
所以x2+2+10+x2=20,
解得x=2.
所以B1M⊥平面ACD1时线段BB1的长为2.
所以PD1=
| 1 |
| 2 |
| 1 |
| 2 |
又因为底面ABCD是直角梯形,∠ABC=∠BAD=90°,
所以AD∥BC∥A1D1,
即PD1∥BC,PD1=BC,
所以四边形BCD1P为平行四边形.
所以BP∥CD1,
又因为BP不在平面ACD1内,
所以BP∥平面ACD1.
(2)连接D1M,B1D1,BM,B1M,
因为B1M⊥平面ACD1,
所以B1M⊥D1M,
所以B1M2+D1M2=B1D12.
又因为B1B⊥平面ABCD,
所以B1B⊥BM.
设B1B=x,由AB=BC=2可得BM=
| 2 |
在Rt△ABC中,可求得DM=
| 10 |
所以D1M2=10+x2.
在Rt△B1A1D1中,可得B1D1=2
| 5 |
所以x2+2+10+x2=20,
解得x=2.
所以B1M⊥平面ACD1时线段BB1的长为2.
点评:本小题主要考查利用线面平行于垂直的判定定理证明线面垂直与线面平行,并且考查空间想象能力和推理论证能力,属于基础题.

练习册系列答案
相关题目
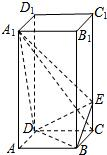 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.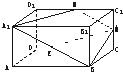 如图,在正四棱柱ABCD-A1B1C1D1中,AA1=
如图,在正四棱柱ABCD-A1B1C1D1中,AA1=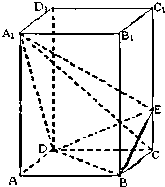 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4, 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC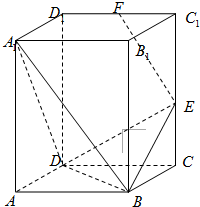 如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是∠DAB=60°的菱形,AA1=4,AB=2,点E在棱CC1上,点F是棱C1D1的中点;
如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是∠DAB=60°的菱形,AA1=4,AB=2,点E在棱CC1上,点F是棱C1D1的中点;