题目内容
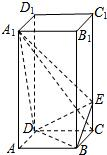 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.(Ⅰ)证明:A1C⊥平面BED;
(Ⅱ)求二面角A1-DE-B的大小.
分析:法一:(Ⅰ)要证A1C⊥平面BED,只需证明A1C与平面BED内两条相交直线BD,EF都垂直;
(Ⅱ)作GH⊥DE,垂足为H,连接A1H,说明∠A1HG是二面角A1-DE-B的平面角,然后解三角形,求二面角A1-DE-B的大小.
法二:建立空间直角坐标系,(Ⅰ)求出
•
=0,
•
=0,证明A1C⊥平面DBE.
(Ⅱ)求出 平面DA1E和平面DEB的法向量,求二者的数量积可求二面角A1-DE-B的大小.
(Ⅱ)作GH⊥DE,垂足为H,连接A1H,说明∠A1HG是二面角A1-DE-B的平面角,然后解三角形,求二面角A1-DE-B的大小.
法二:建立空间直角坐标系,(Ⅰ)求出
| A1C |
| DB |
| A1C |
| DE |
(Ⅱ)求出 平面DA1E和平面DEB的法向量,求二者的数量积可求二面角A1-DE-B的大小.
解答: 解:解法一:
解:解法一:
依题设知AB=2,CE=1.
(Ⅰ)连接AC交BD于点F,则BD⊥AC.
由三垂线定理知,BD⊥A1C.(3分)
在平面A1CA内,连接EF交A1C于点G,
由于
=
=2
,
故Rt△A1AC∽Rt△FCE,∠AA1C=∠CFE,∠CFE与∠FCA1互余.
于是A1C⊥EF.A1C与平面BED内两条相交直线BD,EF都垂直,
所以A1C⊥平面BED.(6分)
(Ⅱ)作GH⊥DE,垂足为H,连接A1H.由三垂线定理知A1H⊥DE,
 故∠A1HG是二面角A1-DE-B的平面角.(8分)
故∠A1HG是二面角A1-DE-B的平面角.(8分)
EF=
=
,CG=
=
,EG=
=
.
=
,GH=
×
=
.
又A1C=
=2
,A1G=A1C-CG=
.tan∠A1HG=
=5
.
所以二面角A1-DE-B的大小为arctan5
.((12分))
解法二:
以D为坐标原点,射线DA为x轴的正半轴,
建立如图所示直角坐标系D-xyz.
依题设,B(2,2,0),C(0,2,0),E(0,2,1),A1(2,0,4).
=(0,2,1),
=(2,2,0),
=(-2,2,-4),
=(2,0,4).(3分)
(Ⅰ)因为
•
=0,
•
=0,
故A1C⊥BD,A1C⊥DE.
又DB∩DE=D,
所以A1C⊥平面DBE.(6分)
(Ⅱ)设向量
=(x,y,z)是平面DA1E的法向量,则n⊥
,n⊥
.
故2y+z=0,2x+4z=0.
令y=1,则z=-2,x=4,
=(4,1,-2).(9分)<
,
>等于二面角A1-DE-B的平面角,cos<
,
=>
=
所以二面角A1-DE-B的大小为arccos
.(12分)
 解:解法一:
解:解法一:依题设知AB=2,CE=1.
(Ⅰ)连接AC交BD于点F,则BD⊥AC.
由三垂线定理知,BD⊥A1C.(3分)
在平面A1CA内,连接EF交A1C于点G,
由于
| AA1 |
| FC |
| AC |
| CE |
| 2 |
故Rt△A1AC∽Rt△FCE,∠AA1C=∠CFE,∠CFE与∠FCA1互余.
于是A1C⊥EF.A1C与平面BED内两条相交直线BD,EF都垂直,
所以A1C⊥平面BED.(6分)
(Ⅱ)作GH⊥DE,垂足为H,连接A1H.由三垂线定理知A1H⊥DE,
 故∠A1HG是二面角A1-DE-B的平面角.(8分)
故∠A1HG是二面角A1-DE-B的平面角.(8分)EF=
| CF2+CE2 |
| 3 |
| CE×CF |
| EF |
| ||
|
| CE2-CG2 |
| ||
| 3 |
| EG |
| EF |
| 1 |
| 3 |
| 1 |
| 3 |
| EF×FD |
| DE |
| ||
|
又A1C=
A
|
| 6 |
5
| ||
| 3 |
| A1G |
| HG |
| 5 |
所以二面角A1-DE-B的大小为arctan5
| 5 |
解法二:
以D为坐标原点,射线DA为x轴的正半轴,
建立如图所示直角坐标系D-xyz.
依题设,B(2,2,0),C(0,2,0),E(0,2,1),A1(2,0,4).
| DE |
| DB |
| A1C |
| DA1 |
(Ⅰ)因为
| A1C |
| DB |
| A1C |
| DE |
故A1C⊥BD,A1C⊥DE.
又DB∩DE=D,
所以A1C⊥平面DBE.(6分)
(Ⅱ)设向量
| n |
| DE |
| DA1 |
故2y+z=0,2x+4z=0.
令y=1,则z=-2,x=4,
| n |
| n |
| A1C |
| n |
| A1C |
| ||||
|
|
| ||
| 42 |
所以二面角A1-DE-B的大小为arccos
| ||
| 42 |
点评:本题考查直线与平面垂直的判定,二面角的求法,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
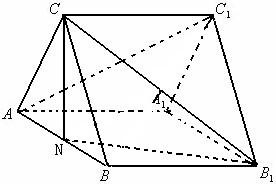 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
