题目内容
用反证法证明命题:若整系数一元二次方程 有有理数根,那么
有有理数根,那么 中至少有一个是偶数,下列假设中正确的是 ( )
中至少有一个是偶数,下列假设中正确的是 ( )
A.假设 都是偶数 都是偶数 | B.假设 都不是偶数 都不是偶数 |
C.假设 至多有一个偶数 至多有一个偶数 | D.假设 至多有两个偶数 至多有两个偶数 |
B
解析试题分析:反证法是“间接证明法”一类,是从反方向证明的证明方法,即:肯定题设而否定结论,从而得出矛盾。若整系数一元二次方程 有有理数根,那么
有有理数根,那么 中至少有一个是偶数,下列假设中正确的是“假设
中至少有一个是偶数,下列假设中正确的是“假设 都不是偶数”。故选B。
都不是偶数”。故选B。
考点:反证法
点评:简单题,反证法是“间接证明法”一类,是从反方向证明的证明方法,即:肯定题设而否定结论,从而得出矛盾。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
用火柴棒摆“金鱼”,如图所示:
按照上面的规律,第 个“金鱼”图需要火柴棒的根数为( )
个“金鱼”图需要火柴棒的根数为( )
A. | B. | C. | D. |
下列推理合理的是( )
A.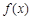 是增函数,则 是增函数,则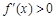 |
B.因为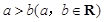 ,则 ,则 |
C.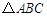 为锐角三角形,则 为锐角三角形,则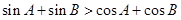 |
D.直线 ,则 ,则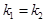 |
有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线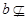 平面
平面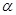 ,直线
,直线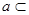 平面
平面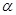 ,直线
,直线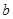 ∥平面
∥平面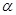 ,则直线
,则直线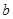 ∥直线
∥直线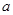 ”的结论显然是错误的,这是因为 ( )
”的结论显然是错误的,这是因为 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
如下图,根据图中的数构成的规律,a所表示的数是( ) 
| A.12 | B.48 | C.60 | D.144 |
用反证法证明命题:“a,b∈N,ab可被5整除,那么a,b中至少有一个能被5整除”时,假设的内容应为( )
| A.a,b都能被5整除 | B.a,b都不能被5整除 |
| C.a,b不都能被5整除 | D.a不能被5整除 |
把1、3、6、10、15、21、…这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形(如图),试求第七个三角形数是( )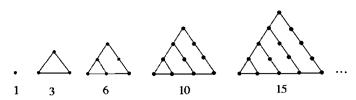
| A.27 | B.28 | C.29 | D.30 |
已知f(x+1)= ,f(1)=1(x∈N*),猜想f(x)的表达式为( )
,f(1)=1(x∈N*),猜想f(x)的表达式为( )
A.f(x)= | B.f(x)= |
C.f(x)= | D.f(x)= |